
【题目】如图1,抛物线y=![]() (x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.
(x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.

(1)求抛物线的解析式;
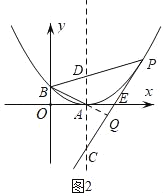
(2)如图2,P是第一象限内抛物线上对称轴右侧一点,过P的直线l与抛物线有且只有一个公共点,l交抛物线对称轴于C点,连PB交对称轴于D点,若∠BAO=∠PCD,求证:AC=2AD;
(3)如图3,以A为顶点作直角,直角边分别与抛物线交于M、N两点,当直角∠MAN绕A点旋转时,求证:MN始终经过一个定点,并求出该定点的坐标.
【答案】(1)y=![]() x2﹣x+1;(2)见解析;(3)定点K的坐标为(2,4)
x2﹣x+1;(2)见解析;(3)定点K的坐标为(2,4)
【解析】
(1)先确定A、B的坐标,然后运用顶点式的待定系数法即可解答;
(2)由(1)得抛物线对称轴为直线x=2.D、C两点在直线x=2上,则设C(2,n),D(2,n');延长BA交直线PC于点Q并设直线PC交x轴于点E.再说明Rt△BOA∽Rt△EAC,进一步可得AC=2AE;然后再说明BQ⊥PC,再求出AB、PC、PB的解析式,最后结合图形即可解答;
(3)过A作垂直于x轴的直线并交MN于点K(2,k),然后再根据旋转的性质设出M(2﹣k,k),最后代入y=![]() (x﹣2)2即可求得k的值,进而确定该点的坐标.
(x﹣2)2即可求得k的值,进而确定该点的坐标.
解:(1)由题意和y=![]() (x﹣m)2设A(m,0)
(x﹣m)2设A(m,0)
当x=0时,y═![]() (0﹣m)2=
(0﹣m)2=![]() ,即设B(0,
,即设B(0,![]() )
)
∴OA=m,OB=![]()
由S△OAB=1
∴![]() OAOB=1,即m
OAOB=1,即m![]() =2
=2
解得,m=2
∴A(2,0),B(0,1)
把y=![]() (x﹣2)2化为一般式为,y=
(x﹣2)2化为一般式为,y=![]() x2﹣x+1.
x2﹣x+1.
(2)由(1)得抛物线对称轴为直线x=2.
D、C两点在直线x=2上,则设C(2,n),D(2,n')
如图2延长BA交直线PC于点Q并设直线PC交x轴于点E.
∵∠BAO=∠PCD,∠BOA=∠EAC=90°
∴Rt△BOA∽Rt△EAC
∴∠BAO=∠ECA
∴tan∠BAO=tan∠ECA=![]()
∴![]() =
=![]()
∴AC=2AE
又∵∠BAO=∠EAQ,∠BAO=∠ECA
∴∠ECA=∠EAQ
又∵∠ECA+∠CEA=90°
∴∠EAQ+∠QEA=90°
∴BQ⊥PC
设直线AB的解析式为y=kx+b,把A(2,0),B(0,1)代入得,
![]() 解得
解得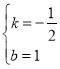
∴直线AB的解析式为,y=﹣![]() x+1
x+1
由BQ⊥PC设直线PC的解析式为y=2x+b'.
又∵过P的直线l与抛物线有且只有一个公共点
∴令2x+b'═![]() (x﹣2)2
(x﹣2)2
整理得,x2﹣12x+4﹣4b'=0,且△=0
即144﹣4(4﹣4b')=0
解得,b'=﹣8
∴直线PC的解析式为,y=2x﹣8.
∴把点C(2,n)代入y=2x﹣8中得,n=2×2﹣8
解得,n=﹣4.
∴C点坐标为(2,﹣4),即AC=4
由AC=2AE得,AE=2.
把b’=﹣8代入方程x2﹣12x+4﹣4b'=0中得,
x2﹣12x+36=0
解得,x1=x2=6
再把x=6代入y=2x﹣8中得,y=2×6﹣8
解得,y=4
∴P(6,4)
设直线PB解析式为y=k'x+1
把P(6,4)代入上式得,4=6k'+1
解得,k'=![]()
∴直线PB的解析式为,y=![]() x+1
x+1
又∵D(2,n')在直线PB上,将其代入y=![]() x+1中得,
x+1中得,
n'=![]() ×2+1=2
×2+1=2
∴D点坐标为(2,2),即AD=2
∴AD=AE
∴AC=2AD
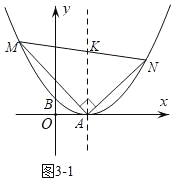
(3)如图3﹣1过A作垂直于x轴的直线并交MN于点K(2,k).
∵∠MAN为直角
∴∠M+∠N=90°,∠MAK+NAK=90°
又∵∠MKA=∠N+∠NAK,∠NKA=∠M+MAK
∴∠MKA+∠NKA=180°
∴直角∠MAN绕A点旋转时,M、K、N三点始终在一条直线上,即MN始终经过一个定点K.
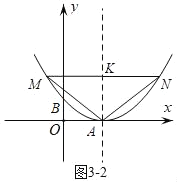
如图3﹣2当MN∥y轴时,此时Rt△MAN为等腰直角三角形,应有AK=MK,则设M(2﹣k,k).
把M(2﹣k,k)代入y=![]() (x﹣2)2中得,k=
(x﹣2)2中得,k=![]() (2﹣k﹣2)2
(2﹣k﹣2)2
解得,k1=0(舍去),k2=4
∴定点K的坐标为(2,4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
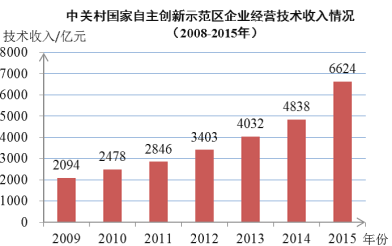
【题目】上图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.
下面四个推断:
①2009 年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是3403亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入平均增长率比2013年到2015年技术收入平均增长率大.
其中,正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
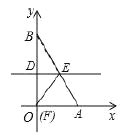
【题目】将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]()
(I)过边![]() 上的动点
上的动点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于点
于点![]() ,沿着
,沿着![]() 折叠该纸片,点
折叠该纸片,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处.
处.
①如图,当![]() 为
为![]() 中点时,求
中点时,求![]() 点的坐标;
点的坐标;
②连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 点坐标:
点坐标:
(Ⅱ)![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线折叠,得到
所在的直线折叠,得到![]() ,连接
,连接![]() ,当
,当![]() 取得最小值时,求
取得最小值时,求![]() 点坐标(直接写出结果即可).
点坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列结论:
①二次函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
②关于![]() 的方程
的方程![]() 的解是
的解是![]() ,
,![]() (
(![]() 、
、![]() 、
、![]() 均为常数,
均为常数,![]() ),则方程
),则方程![]() 的解是
的解是![]() ,
,![]() .
.
③设二次函数![]() ,当
,当![]() 时,总有
时,总有![]() ,当
,当![]() 时,总有
时,总有![]() ,那么
,那么![]() 的取值范围是
的取值范围是![]() .
.
其中,正确结论的个数是( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学位为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表.
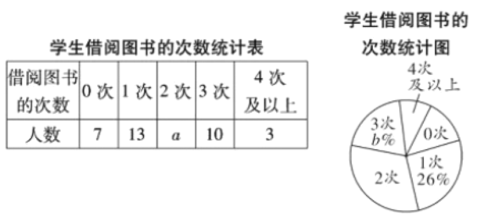
请你根据统计图表中的信息,解答下列问题:
(1)![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)该调查统计数据的中位数是_________,众数是__________;
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点A (-4,-2),将点A向右平移6个单位长度,得到点B.

(1)若抛物线y=-x2+bx+c经过点A,B,求此时抛物线的表达式;
(2)在(1)的条件下的抛物线顶点为C,点D是直线BC上一动点(不与B,C重合),是否存在点D,使△ABC和以点A,B,D构成的三角形相似?若存在,请求出此时D的坐标;若不存在,请说明理由;
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动,当抛物线与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标t的取值范围.
有且只有一个公共点时,求抛物线顶点横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
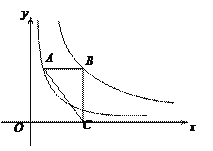
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
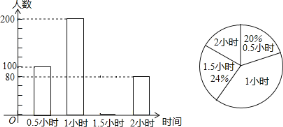
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
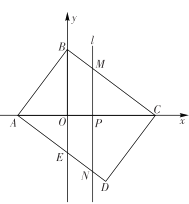
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 动点
动点![]() 从原点出发,以每秒 1 个单位长度的速度沿
从原点出发,以每秒 1 个单位长度的速度沿![]() 轴正方向移动,移动时间为
轴正方向移动,移动时间为![]() 秒,过点 P 作垂直于
秒,过点 P 作垂直于![]() 轴的直线
轴的直线![]() ,交
,交![]() 于点 M ,交
于点 M ,交![]() 或
或![]() 于点 N ,直线
于点 N ,直线![]() 扫过矩形
扫过矩形![]() 的面积为
的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 移动过程中到点
移动过程中到点![]() 之前的
之前的![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在直线![]() 移动过程中,第一象限的直线
移动过程中,第一象限的直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰直角三角形? 若存在,直接写出点
是等腰直角三角形? 若存在,直接写出点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com