
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxoyжаЃЌЕуA (-4,-2)ЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуB.

ЃЈ1ЃЉШєХзЮяЯпyЃН-x2ЃЋbxЃЋcОЙ§ЕуA,BЃЌЧѓДЫЪБХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЕФХзЮяЯпЖЅЕуЮЊCЃЌЕуDЪЧжБЯпBCЩЯвЛЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌЪЧЗёДцдкЕуDЃЌЪЙЁїABCКЭвдЕуA,B,DЙЙГЩЕФШ§НЧаЮЯрЫЦЃПШєДцдкЃЌЧыЧѓГіДЫЪБDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєХзЮяЯпyЃН-x2ЃЋbxЃЋcЕФЖЅЕудкжБЯпyЃНxЃЋ2ЩЯвЦЖЏЃЌЕБХзЮяЯпгыЯпЖЮ![]() гаЧвжЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯпЖЅЕуКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
гаЧвжЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯпЖЅЕуКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН-x2-2xЃЋ6ЃЛЃЈ2ЃЉДцдкЃЌD (![]() ,
,![]() )ЃЛЃЈ3ЃЉ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
)ЃЛЃЈ3ЃЉ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЕФзјБъНсКЯЯпЖЮABЕФГЄЖШЃЌПЩЕУГіЕуBЕФзјБъЃЌИљОнЕуAЃЌBЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉгЩХзЮяЯпНтЮіЪНЃЌЧѓГіЖЅЕуCЕФзјБъЃЌДгЖјЧѓГіжБЯпBCНтЮіЪНЃЌЩшD (d,-3d+4)ЃЌ
ИљОнвбжЊПЩжЊAD=AB=6ЪБЃЌЁїABCЁзЁїBADЃЌДгЖјСаГіЙигкdЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓНтЃЛ
ЃЈ3ЃЉНЋХзЮяЯпЕФБэДяЪНБфаЮЮЊЖЅЕуЪБЃЌвРДЫДњШыЕуAЃЌBЕФзјБъЧѓГіtЕФжЕЃЌдйНсКЯЭМаЮМДПЩЕУГіЃКЕБХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЪБtЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉЁпЕуAЕФзјБъЮЊЃЈ-4ЃЌ-2ЃЉЃЌНЋЕуAЯђгвЦНвЦ6ИіЕЅЮЛГЄЖШЕУЕНЕуBЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ2ЃЌ-2ЃЉЃЎ
ЁпХзЮяЯпyЃН-x2+bxЃЋcЙ§Еу![]() ЃЌ
ЃЌ
Ёр![]() , НтЕУ
, НтЕУ![]()
ЁрХзЮяЯпБэДяЪНЮЊyЃН-x2-2xЃЋ6
ЃЈ2ЃЉДцдк.
ШчЭМ
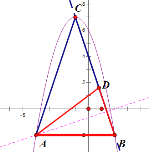
гЩЃЈ1ЃЉЕУЃЌyЃН-x2-2xЃЋ6ЃН-(x+1)2ЃЋ7ЃЌ
ЁрC (-1,7)
ЩшжБЯпBCНтЮіЪНЮЊyЃНkxЃЋb
Ёр![]() НтжЎЕУЃЌ
НтжЎЕУЃЌ![]()
ЁрlBCЃКyЃН-3xЃЋ4
ЩшD (d,-3d+4)ЃЌ
ЁпдкЁїABCжаAC=BC
ЁрЕБЧвНіЕБAD=AB=6ЪБЃЌСНШ§НЧаЮЯрЫЦ
МД(-4-d)2+(-2+3d-4)2=36ЪБЃЌЁїABCЁзЁїBADЃЌ
НтжЎЕУЃЌd1=![]() ЁЂd2=2(ЩсШЅ)
ЁЂd2=2(ЩсШЅ)
ЁрДцдкЕуDЃЌЪЙЁїABCКЭвдЕуA,B,DЙЙГЩЕФШ§НЧаЮЯрЫЦЃЌДЫЪБЕуD (![]() ,
,![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉШчЭМЃК
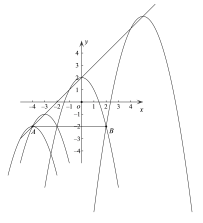
ХзЮяЯпyЃН-x2+bxЃЋcЖЅЕудкжБЯп![]() ЩЯ
ЩЯ
ЁрХзЮяЯпЖЅЕузјБъЮЊ![]()
ЁрХзЮяЯпБэДяЪНПЩЛЏЮЊ![]() ЃЎ
ЃЎ
Аб![]() ДњШыБэДяЪНПЩЕУ
ДњШыБэДяЪНПЩЕУ![]()
НтЕУ![]() ЃЎ
ЃЎ
гжЁпХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЃЌ
Ёр-4ЁмtЃМ-3ЃЎ
Аб![]() ДњШыБэДяЪНПЩЕУ
ДњШыБэДяЪНПЩЕУ![]() ЃЎ
ЃЎ
НтЕУ![]() ЃЌ
ЃЌ
гжЁпХзЮяЯпгыЯпЖЮABгаЧвжЛгавЛИіЙЋЙВЕуЃЌ
Ёр0ЃМtЁм5ЃЎ
злЩЯПЩжЊ![]() ЕФШЁжЕЗЖЮЇЪБ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ
ЕФШЁжЕЗЖЮЇЪБ-4ЁмtЃМ-3Лђ0ЃМtЁм5ЃЎ


 вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
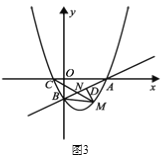
ЁОЬтФПЁПШчЭМ![]() ЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕ
ЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсЕФСэвЛНЛЕуЮЊЕу
жсЕФСэвЛНЛЕуЮЊЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЂйШчЭМ2ЫљЪОЃЌжБЯп![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
Ђк ШчЭМ3ЫљЪОЃЌСЌНг![]() Й§Еу
Й§Еу![]() зї
зї![]() гк
гк![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() жаЕФФГИіНЧЧЁКУЕШгк
жаЕФФГИіНЧЧЁКУЕШгк![]() ЕФ2БЖЃПШєДцдкЃЌЧѓЕу
ЕФ2БЖЃПШєДцдкЃЌЧѓЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛИіжБНЧШ§НЧаЮжНЦЌ![]() ЃЌЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕу
ЃЌЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌЕу
ЃЌЕу![]()
(I)Й§Бп![]() ЩЯЕФЖЏЕу
ЩЯЕФЖЏЕу![]() (Еу
(Еу![]() ВЛгыЕу
ВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯ)зї
жиКЯ)зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌбизХ
ЃЌбизХ![]() елЕўИУжНЦЌЃЌЕу
елЕўИУжНЦЌЃЌЕу![]() ТфдкЩфЯп
ТфдкЩфЯп![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ДІЃЎ
ДІЃЎ
ЂйШчЭМЃЌЕБ![]() ЮЊ
ЮЊ![]() жаЕуЪБЃЌЧѓ
жаЕуЪБЃЌЧѓ![]() ЕуЕФзјБъЃЛ
ЕуЕФзјБъЃЛ
ЂкСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌЧѓ
ЮЊжБНЧШ§НЧаЮЪБЃЌЧѓ![]() ЕузјБъЃК
ЕузјБъЃК
(Ђђ)![]() ЪЧ
ЪЧ![]() БпЩЯЕФЖЏЕу(Еу
БпЩЯЕФЖЏЕу(Еу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯ)ЃЌНЋ
жиКЯ)ЃЌНЋ![]() би
би![]() ЫљдкЕФжБЯпелЕўЃЌЕУЕН
ЫљдкЕФжБЯпелЕўЃЌЕУЕН![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ШЁЕУзюаЁжЕЪБЃЌЧѓ
ШЁЕУзюаЁжЕЪБЃЌЧѓ![]() ЕузјБъ(жБНгаДГіНсЙћМДПЩ)ЃЎ
ЕузјБъ(жБНгаДГіНсЙћМДПЩ)ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуA(Љ3ЃЌy1)ЃЌB(2ЃЌy2)ОљдкХзЮяЯпyЃНax2+bx+cЩЯЃЌЕуP(mЃЌn)ЪЧИУХзЮяЯпЕФЖЅЕуЃЌШєy1ЃОy2ЁнnЃЌдђmЕФШЁжЕЗЖЮЇЪЧ(ЁЁЁЁ)
A.Љ3ЃМmЃМ2B.Љ![]() ЃМmЃМ-
ЃМmЃМ-![]() C.mЃОЉ
C.mЃОЉ![]() D.mЃО2
D.mЃО2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
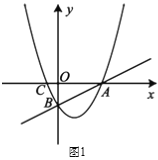
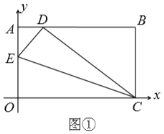
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃН![]() ЃЈxЉmЃЉ2ЕФЖЅЕуAдкxжсе§АыжсЩЯЃЌНЛyжсгкBЕуЃЌSЁїOABЃН1ЃЎ
ЃЈxЉmЃЉ2ЕФЖЅЕуAдкxжсе§АыжсЩЯЃЌНЛyжсгкBЕуЃЌSЁїOABЃН1ЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
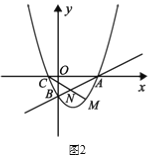
ЃЈ2ЃЉШчЭМ2ЃЌPЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЖдГЦжсгвВрвЛЕуЃЌЙ§PЕФжБЯпlгыХзЮяЯпгаЧвжЛгавЛИіЙЋЙВЕуЃЌlНЛХзЮяЯпЖдГЦжсгкCЕуЃЌСЌPBНЛЖдГЦжсгкDЕуЃЌШєЁЯBAOЃНЁЯPCDЃЌЧѓжЄЃКACЃН2ADЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌвдAЮЊЖЅЕузїжБНЧЃЌжБНЧБпЗжБ№гыХзЮяЯпНЛгкMЁЂNСНЕуЃЌЕБжБНЧЁЯMANШЦAЕуа§зЊЪБЃЌЧѓжЄЃКMNЪМжеОЙ§вЛИіЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛОиаЮжНЦЌ![]() ЗХдкжБНЧзјБъЯЕжаЃЌ
ЗХдкжБНЧзјБъЯЕжаЃЌ![]() ЮЊдЕуЃЌ
ЮЊдЕуЃЌ![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШчЭМЂйЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпЩЯЕФ
БпЩЯЕФ![]() ЕуЃЌЧѓ
ЕуЃЌЧѓ![]() ЕуЕФзјБъЃЛ
ЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌдк![]() ЁЂ
ЁЂ![]() БпЩЯбЁШЁЪЪЕБЕФЕу
БпЩЯбЁШЁЪЪЕБЕФЕу![]() ЁЂ
ЁЂ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЪЙ
елЕўЃЌЪЙ![]() ЕуТфдк
ЕуТфдк![]() БпЩЯ
БпЩЯ![]() ЕуЃЌЙ§
ЕуЃЌЙ§![]() зї
зї![]() НЛ
НЛ![]() гк
гк![]() ЕуЃЌНЛ
ЕуЃЌНЛ![]() гк
гк![]() ЕуЃЌЩш
ЕуЃЌЩш![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ

ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎЃЈжБНгаДГіНсЙћМДПЩЃЉ
ЕФУцЛ§ЃЎЃЈжБНгаДГіНсЙћМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ ![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛЕуЃЌСЌНг
ЩЯЕФвЛЕуЃЌСЌНг![]() Й§Еу
Й§Еу![]() зї
зї![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
![]() ЕБЕу
ЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌШчЭМЂйЃЌЧѓжЄЃК
ЩЯЪБЃЌШчЭМЂйЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
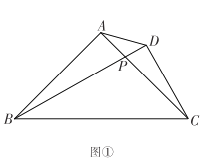
![]() ЕБЕу
ЕБЕу![]() дкжБЯп
дкжБЯп![]() ЩЯвЦЖЏЪБЃЌЮЛжУШчЭМЂкЁЂЭМЂлЫљЪОЃЌЯпЖЮ
ЩЯвЦЖЏЪБЃЌЮЛжУШчЭМЂкЁЂЭМЂлЫљЪОЃЌЯпЖЮ![]() гы
гы![]() жЎМфгжгадѕбљЕФЪ§СПЙиЯЕЃПЧыжБНгаДГіФуЕФВТЯыЃЌВЛашжЄУїЃЎ
жЎМфгжгадѕбљЕФЪ§СПЙиЯЕЃПЧыжБНгаДГіФуЕФВТЯыЃЌВЛашжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
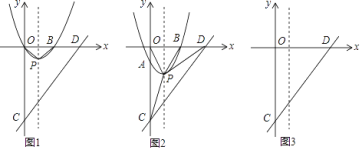
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=x2Љ2xгыxжсНЛгкOЁЂBСНЕуЃЌЖЅЕуЮЊPЃЌСЌНгOPЁЂBPЃЌжБЯпy=xЉ4гыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуDЃЎ
ЃЈ1ЃЉаДГіЕуBзјБъЃЛХаЖЯЁїOBPЕФаЮзДЃЛ
ЃЈ2ЃЉНЋХзЮяЯпбиЖдГЦжсЦНвЦmИіЕЅЮЛГЄЖШЃЌЦНвЦЕФЙ§ГЬжаНЛyжсгкЕуAЃЌЗжБ№СЌНгCPЁЂDPЃЛ
ЃЈiЃЉШєХзЮяЯпЯђЯТЦНвЦmИіЕЅЮЛГЄЖШЃЌЕБSЁїPCD= ![]() SЁїPOCЪБЃЌЧѓЦНвЦКѓЕФХзЮяЯпЕФЖЅЕузјБъЃЛ
SЁїPOCЪБЃЌЧѓЦНвЦКѓЕФХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈiiЃЉдкЦНвЦЙ§ГЬжаЃЌЪдЬНОПSЁїPCDКЭSЁїPODжЎМфЕФЪ§СПЙиЯЕЃЌжБНгаДГіЫќУЧжЎМфЕФЪ§СПЙиЯЕМАЖдгІЕФmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїBCEжаЃЌЕуAЪЧБпBEЩЯвЛЕуЃЌвдABЮЊжБОЖЕФЁбOгыCEЯрЧагкЕуDЃЌADЁЮOCЃЌЕуFЮЊOCгыЁбOЕФНЛЕуЃЌСЌНгAF.
ЃЈ1ЃЉЧѓжЄЃКCBЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯECB=60ЁуЃЌAB=6ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com