
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,
为原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() .
.
(1)如图①,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 点,求
点,求![]() 点的坐标;
点的坐标;
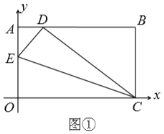
(2)如图②,在![]() 、
、![]() 边上选取适当的点
边上选取适当的点![]() 、
、![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上
边上![]() 点,过
点,过![]() 作
作![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,设
点,设![]() 的坐标为
的坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;

(3)在(2)的条件下,若![]() ,求
,求![]() 的面积.(直接写出结果即可)
的面积.(直接写出结果即可)
【答案】(1)![]() (2)
(2)![]() (
(![]() ) (3)
) (3)![]()
【解析】
(1)由折叠的性质可知![]() ,然后设
,然后设![]() ,在
,在![]() 中利用勾股定理即可求出m的值,从而可确定E点的坐标;
中利用勾股定理即可求出m的值,从而可确定E点的坐标;
(2)连接OT,由折叠的性质可知![]() ,然后在
,然后在![]() 中利用勾股定理即可得到
中利用勾股定理即可得到![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)先根据OG的长度求出![]() 的长度,然后设
的长度,然后设![]() ,则
,则![]() ,在
,在![]() 中,利用勾股定理即可求出x的值,最后利用
中,利用勾股定理即可求出x的值,最后利用![]() 即可求解.
即可求解.
解:(1)∵四边形OABC是矩形,
∴![]() .
.
设![]() ,则
,则![]() ,
,
由折叠的性质可知![]() ,
,![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)连接![]() ,
,

由折叠的性质可知![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,即
,即![]() ,
,
自变量![]() 的取值范围是
的取值范围是![]() .
.
(3)∵![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() .
.
由折叠的性质可知![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,
由勾股定理得![]() ,
,
∴![]() ,
,
解得![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形的边长均为1,线段 AB的两个端点均在小正方形的顶点上.
(1)在图中画出以AB为直角边的Rt△ABC,点C在小正方形的顶点上,且Rt△ABC的面积为5;
(2)在(1)的条件下,画出△BCD,点D在小正方形的顶点上,且tan∠CDB![]() ,连接AD,请直接写出线段AD的长.
,连接AD,请直接写出线段AD的长.
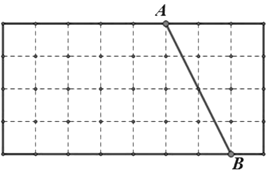
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径.某校为了解本校学生课外阅读情况,对九年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请根据图中提供的信息,解答下面的问题:
(1)本次抽样调查的样本容量是____ ____;
(2)在条形统计图补中,计算出日人均阅读时间在0.5~1小时的人数是____ ____,并将条形统计图补充完整;
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数____ ____度;
(4)根据本次抽样调查,试估计该市15000名九年级学生中日人均阅读时间在0.5~1.5小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点A (-4,-2),将点A向右平移6个单位长度,得到点B.

(1)若抛物线y=-x2+bx+c经过点A,B,求此时抛物线的表达式;
(2)在(1)的条件下的抛物线顶点为C,点D是直线BC上一动点(不与B,C重合),是否存在点D,使△ABC和以点A,B,D构成的三角形相似?若存在,请求出此时D的坐标;若不存在,请说明理由;
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动,当抛物线与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标t的取值范围.
有且只有一个公共点时,求抛物线顶点横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初三学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.

![]() 求这次调查的家长人数,并补全条形图;
求这次调查的家长人数,并补全条形图;
![]() 求扇形图中表示家长“赞成”的圆心角的度数;
求扇形图中表示家长“赞成”的圆心角的度数;
![]() 若某地区共有初三学生
若某地区共有初三学生![]() 名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少?
名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=BC,点D、E分别在边BC,AC上,连接DE,且DE=DC.

(1)问题发现:若∠ACB=∠ECD=45°,则![]() = .
= .
(2)拓展探究:若∠ACB=∠ECD=30°,将△EDC饶点C按逆时针旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中![]() 的大小有无变化?如果不变,请求出
的大小有无变化?如果不变,请求出![]() 的值,如果变化,请说明理由;
的值,如果变化,请说明理由;
(3)问题解决:若∠ABC=∠EDC=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则![]() 的值为 .(用含β的式子表示)
的值为 .(用含β的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读下列材料,然后回答问题:
如果a>0,b>0,那么(![]() -
-![]() )2≥0,即a+b-2
)2≥0,即a+b-2![]() ≥0 得
≥0 得![]() ≥
≥![]() ,其中,当a=b时取等号,我们把
,其中,当a=b时取等号,我们把![]() 称为a、b的算术平均数,
称为a、b的算术平均数, ![]() 称为a、b的几何平均数.
称为a、b的几何平均数.
如果a>0,b>0,c>0,同样可以得到![]() ≥
≥![]() ,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
(1)设剪去的小正方形边长为x cm,无盖纸盒的容积为V,求V与x的函数关系式及x的取值范围.
(2)当x为何值时,容积V有最大值,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与x轴、y轴分别交于A、B两点,设O为坐标原点.
与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线![]() 平行,求直线l的解析式.
平行,求直线l的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com