
【题目】先仔细阅读下列材料,然后回答问题:
如果a>0,b>0,那么(![]() -
-![]() )2≥0,即a+b-2
)2≥0,即a+b-2![]() ≥0 得
≥0 得![]() ≥
≥![]() ,其中,当a=b时取等号,我们把
,其中,当a=b时取等号,我们把![]() 称为a、b的算术平均数,
称为a、b的算术平均数, ![]() 称为a、b的几何平均数.
称为a、b的几何平均数.
如果a>0,b>0,c>0,同样可以得到![]() ≥
≥![]() ,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
(1)设剪去的小正方形边长为x cm,无盖纸盒的容积为V,求V与x的函数关系式及x的取值范围.
(2)当x为何值时,容积V有最大值,最大值是多少?

科目:初中数学 来源: 题型:
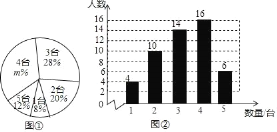
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,
为原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() .
.
(1)如图①,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 点,求
点,求![]() 点的坐标;
点的坐标;
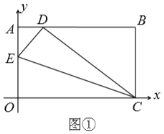
(2)如图②,在![]() 、
、![]() 边上选取适当的点
边上选取适当的点![]() 、
、![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上
边上![]() 点,过
点,过![]() 作
作![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,设
点,设![]() 的坐标为
的坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;

(3)在(2)的条件下,若![]() ,求
,求![]() 的面积.(直接写出结果即可)
的面积.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
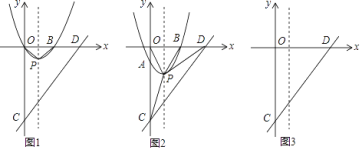
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
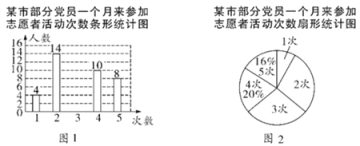
(1) “![]() 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;
(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于![]() 次的概率;
次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为![]() ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为![]() ,当
,当![]() 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
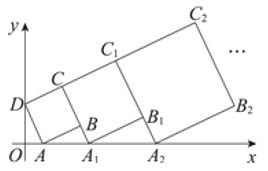
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;…,按照这样的规律作正方形,则点
;…,按照这样的规律作正方形,则点![]() 的纵坐标为__________.
的纵坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
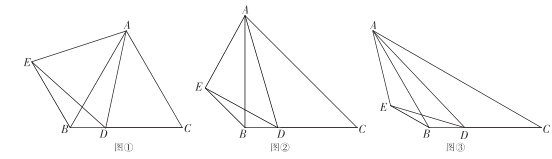
【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接![]() .
.
(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
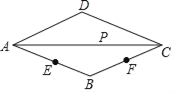
【题目】如图,四边形ABCD是菱形.AB=5,点P是对角线AC上任意一点,E、F分别是AB、BC边上的中点.当点P在线段AC上移动时,则PE+PF的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com