
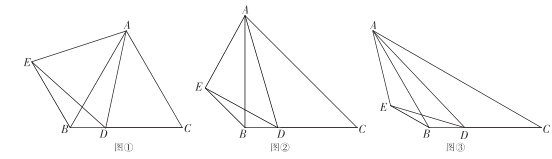
【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接![]() .
.
(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
【答案】(1)见解析;(2)图②的结论是:![]() ;图 ③ 的结论是:
;图 ③ 的结论是:![]() ,证明过程见解析.
,证明过程见解析.
【解析】
(1)△EAD为等腰三角形,当∠ABC=60°=∠AED时,可推出△AED为等边三角形,进一步证明△AEB≌△ADC,即得到CD=BE;
(2)当∠ABC=90°=∠AED时,此时△AED、△ABC变成等腰直角三角形,∴∠EAD=∠BAC=45°,可推出∠EAB=∠DAC,且![]() ,故可证明△AEB∽△ADC,即可得到
,故可证明△AEB∽△ADC,即可得到![]() ;
;
当∠ABC=120°=∠AED时,此时△AED、△ABC变成30°、30°、120°的等腰三角形,同样可证明△AEB∽△ADC,即可得到![]() .
.
解:(1) 证明:∵△EAD为等腰三角形,且∠ABC=60°=∠AED,
∴△AED变成等边三角形,∴∠EAD=∠BAC,
又∠EAB=60°-∠BAD,∠DAC=60°-∠BAD
∴∠EAB=∠DAC,
在△AEB和△ADC中:

∴△AEB≌△ADC,
∴CD=BE.
(2)图②的结论是:![]()
图③的结论是:![]() .
.
下面选择图②进行证明:
证明:![]()
∴△AED,△ABC都是等腰直角三角形,
∴∠CAD+∠DAB=∠EAB+∠BAD=45°
∴∠CAD=∠BAE
![]()
∴△BAE∽△CAD
![]() .
.
故答案为:![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读下列材料,然后回答问题:
如果a>0,b>0,那么(![]() -
-![]() )2≥0,即a+b-2
)2≥0,即a+b-2![]() ≥0 得
≥0 得![]() ≥
≥![]() ,其中,当a=b时取等号,我们把
,其中,当a=b时取等号,我们把![]() 称为a、b的算术平均数,
称为a、b的算术平均数, ![]() 称为a、b的几何平均数.
称为a、b的几何平均数.
如果a>0,b>0,c>0,同样可以得到![]() ≥
≥![]() ,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
,其中,当a=b=c时取等号于是就有定理:几个正数的算术平均数不小于它们的几何平均数.请用上述定理解答问题:把边长为30 cm的正方形纸片的4角各剪去一个小正方形,折成无盖纸盒(如图)
(1)设剪去的小正方形边长为x cm,无盖纸盒的容积为V,求V与x的函数关系式及x的取值范围.
(2)当x为何值时,容积V有最大值,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一动点,
上一动点,![]() 且
且![]() ,连接
,连接![]() ,其中
,其中![]() .
.
问题发现:(1)如图1,若![]() ,
,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?直接写出答案;
的值为多少?直接写出答案;
类比探究,(2)如图2,若![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?请说明理由.
的值为多少?请说明理由.
拓展应用:(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,以
上一点,以![]() 为边,在如图所示位置作正方形
为边,在如图所示位置作正方形![]() ,点
,点![]() 为正方形
为正方形![]() 的对称中心,且
的对称中心,且![]() ,请直接写出
,请直接写出![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与x轴、y轴分别交于A、B两点,设O为坐标原点.
与x轴、y轴分别交于A、B两点,设O为坐标原点.
(1)求∠ABO的正切值;
(2)如果点A向左平移12个单位到点C,直线l过点C且与直线![]() 平行,求直线l的解析式.
平行,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
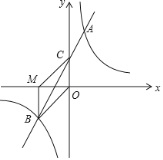
(1)求该反比例函数和一次函数的解析式;
(2)连接AO,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com