【题目】在抗击新型冠状病毒肺炎战役中，某市党员积极响应国家号召参加志愿者活动，为人民服务，现随机抽查部分党员一个月来参加志愿者活动的次数，并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2)．

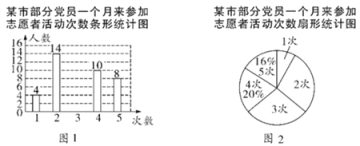
（1） “次”所在扇形的圆心角度数是 ，请补全 条形统计图；

（2）若从抽在的党员中随机选择一位接受媒体的采访，求该党员一个月来参加志愿者活动次数不少于次的概率；

（3）设随机抽查的党员一个月来参加志愿者活动次数的中位数为，若去掉一部分党员参加志愿者活动的次数后，得到一组新数据的众数为，当时，求最少去掉了几名党员参加志愿者活动的次数．

参考答案：

【答案】（1），补全条形统计图如解图所示见解析；（2）（该党员一个月来参加志愿者活动次数不少于次）；（3）去掉个参加志愿者活动次数为次的和个参加志愿者活动次数为次的．

【解析】

（1）根据扇形统计图可知“4次”的人数占比为20%，即可出圆心角度数；根据“4次”人数占比，求出总人数，进而可以求得“3”次的人数；

（2）（该党员一个月来参加志愿者活动次数不少于次）=少于3次的人数总人数；

（3）首先求出中位数，根据题意，使得新数据的众数，得到b=4或者5，再比较需要去掉的人数，取最少去掉的人数即可．

（1）由扇形统计图知“4次”的人数占比为20%，

∴“4次”所在圆心角的度数为36020%=72．

随机抽查的党员人数为 (人)，

∴“3次”的人数为50-4-14-10-8=14(人)

补全条形统计图如图所示：

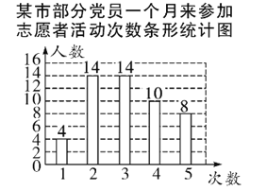
（2）∵随机抽查的党员人数为 (人)，其中参加志愿者活动次数不少于次的有14+10+8=32（人），

∴P（该党员一个月来参加志愿者活动次数不少于3次）．

（3）将参加次数按由小到大进行排列，可得中位数为第25、26个数的平均数，由题意得，

∵去掉一部分党员参加志愿者活动的次数后，得到一组新数据的众数为，且，

∴或5，当时，最少需去掉10名党员参加志愿者活动的次数，

即去掉个参加志愿者活动次数为次的和个参加志愿者活动次数为次的，

当时，最少需去掉17名党员参加志愿者活动的次数，

即去掉7个参加活动为2次的，7个参加活动为3次的，3个参加活动为4次的，

∵1017

∴b=4．

这时最少去掉了10名党员这一个月来参加志愿者活动的次数．

即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的．

关闭