
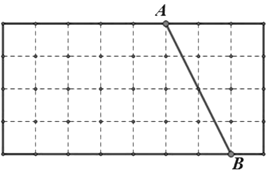
【题目】如图,方格纸中的每个小正方形的边长均为1,线段 AB的两个端点均在小正方形的顶点上.
(1)在图中画出以AB为直角边的Rt△ABC,点C在小正方形的顶点上,且Rt△ABC的面积为5;
(2)在(1)的条件下,画出△BCD,点D在小正方形的顶点上,且tan∠CDB![]() ,连接AD,请直接写出线段AD的长.
,连接AD,请直接写出线段AD的长.
科目:初中数学 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了![]() 名学生(每名学生必选且只能选择这五项活动中的一种).
名学生(每名学生必选且只能选择这五项活动中的一种).
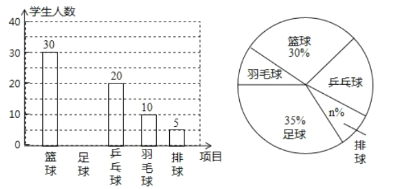
根据以上统计图提供的信息,请解答下列问题:
(1)![]() ,
,![]() .
.
(2)补全上图中的条形统计图.
(3)若全校共有![]() 名学生,请求出该校约有多少名学生喜爱打乒乓球.
名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的![]() 名学生中,有小薇、小燕、小红、小梅等
名学生中,有小薇、小燕、小红、小梅等![]() 名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这
名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这![]() 名女生中,选取
名女生中,选取![]() 名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母
名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母![]() 、
、![]() 、
、![]() 、
、![]() 代表)
代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
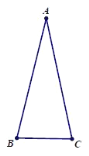
【题目】如图,![]() 中,
中,![]() .
.![]() . 将
. 将![]() 绕点
绕点![]() 顺时针旋转60°到点
顺时针旋转60°到点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,
,![]() .
.
(1)依题意补全图形:
(2)判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)请问在直线![]() 上是否存在点
上是否存在点![]() .使得
.使得![]() 恒成立若存在,请用文字描述出点
恒成立若存在,请用文字描述出点![]() 的准确位置,并画图证明;若不存在,请说明理由.
的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
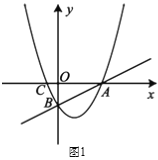
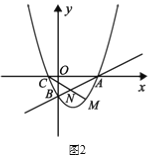
【题目】如图![]() 所示,在平面直角坐标系
所示,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一交点为点
轴的另一交点为点![]() .
.
(1)求抛物线的函数表达式;
(2)点![]() 为直线
为直线![]() 下方抛物线上一动点.
下方抛物线上一动点.
①如图2所示,直线![]() 交线段
交线段![]() 于点
于点![]() ,求
,求![]() 的最小值;
的最小值;
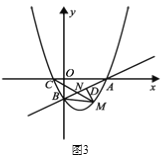
② 如图3所示,连接![]() 过点
过点![]() 作
作![]() 于
于![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,求点
的2倍?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
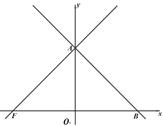
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线yx m交 y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
(1)求∠FAB的度数;
(2)点 P是线段OB上一点,过点P作 PQ⊥OB交直线 FA于点Q,连接 BQ,取 BQ的中点C,连接AP、AC、CP,过点C作 CR⊥AP于点R,设 BQ的长为d,CR的长为h,求d与 h的函数关系式(不要求写出自变量h的取值范围);
(3)在(2)的条件下,过点 C 作 CE⊥OB于点E,CE交 AB于点D,连接 AE,∠AEC=2∠DAP,EP=2,作线段 CD 关于直线AB的对称线段DS,求直线PS与直线 AF的交点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再填空解题:
(1)方程:![]() 的根是:
的根是:![]() ________,
________,![]() ________,则
________,则![]() ________,
________,![]() ________.
________.
(2)方程![]() 的根是:
的根是:![]() ________,
________,![]() ________,则
________,则![]() ________,
________,![]() ________.
________.
(3)方程![]() 的根是:
的根是:![]() ________,
________,![]() ________,则
________,则![]() ________,
________,![]() ________.
________.
(4)如果关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 且
且![]() 、
、![]() 、
、![]() 为常数)的两根为
为常数)的两根为![]() ,
,![]() ,
,
根据以上(1)(2)(3)你能否猜出:![]() ,
,![]() 与系数
与系数![]() 、
、![]() 、
、![]() 有什么关系?请写出来你的猜想并说明理由.
有什么关系?请写出来你的猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
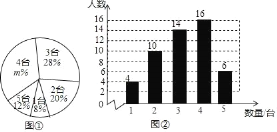
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
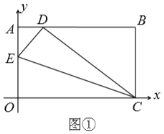
【题目】将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,
为原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() .
.
(1)如图①,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 点,求
点,求![]() 点的坐标;
点的坐标;
(2)如图②,在![]() 、
、![]() 边上选取适当的点
边上选取适当的点![]() 、
、![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上
边上![]() 点,过
点,过![]() 作
作![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,设
点,设![]() 的坐标为
的坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;

(3)在(2)的条件下,若![]() ,求
,求![]() 的面积.(直接写出结果即可)
的面积.(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com