
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��yx m�� y����������ڵ�A����x����������ڵ�B������A��ֱ��AF��x��ĸ������ڵ�F����AFO=45����
��1�����FAB�Ķ�����
��2���� P���߶�OB��һ�㣬����P�� PQ��OB��ֱ�� FA�ڵ�Q������ BQ��ȡ BQ���е�C������AP��AC��CP������C�� CR��AP�ڵ�R���� BQ�ij�Ϊd��CR�ij�Ϊh����d�� h�ĺ�����ϵʽ����Ҫ��д���Ա���h��ȡֵ��Χ����
��3���ڣ�2���������£����� C �� CE��OB�ڵ�E��CE�� AB�ڵ�D������ AE����AEC=2��DAP��EP=2�����߶� CD ����ֱ��AB�ĶԳ��߶�DS����ֱ��PS��ֱ�� AF�Ľ���K�����꣮

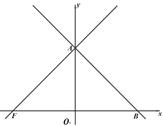
���𰸡���1����FAB=90������2��![]() ����3��ֱ��PS��ֱ��AF�Ľ���K(-2��6)��
����3��ֱ��PS��ֱ��AF�Ľ���K(-2��6)��
��������
��1��ͨ��ֱ��AB�Ľ���ʽ�������A��B�����꣬��֪![]() �ǵ���ֱ�������Σ��ٽ����֪��������ȷ��
�ǵ���ֱ�������Σ��ٽ����֪��������ȷ��![]() ��
��
��2��������֪����֤��CP=AC=QC=BC�Ӷ��ó���ACP �ǵ���ֱ�������Σ���Rt��CRP�У�����sin��CPR![]() ���Ƴ�
���Ƴ�![]() ���̶��ó�
���̶��ó�![]() ���ó��𰸣�
���ó��𰸣�
��3������ A ��AH��CE �� EC ���ӳ����ڵ� H���ӳ� CH ���� G��ʹ HG=CH������AG��֤����AHC�ա�CEP����![]() ���ó�EG=CE+CH+GH=n+2+2=n+4����ͨ���ǵĵ����������ó���EAG=��G���Ӷ���EG=EA=n+4����Rt��AHE �У�ͨ�����ɶ���AE=HE+AH�����n��ֵΪ6���Ӷ��ó�ֱ��AF�Ľ���ʽy x 8 �������ֱ��
���ó�EG=CE+CH+GH=n+2+2=n+4����ͨ���ǵĵ����������ó���EAG=��G���Ӷ���EG=EA=n+4����Rt��AHE �У�ͨ�����ɶ���AE=HE+AH�����n��ֵΪ6���Ӷ��ó�ֱ��AF�Ľ���ʽy x 8 �������ֱ��
PS�Ľ���ʽΪ y=-x+4���㼴�ɣ�
�⣺��1������ͼ��y x m ����x=0ʱ��y=m
��A��0��m����OA=m
��y=0ʱ��0=-x+m��x=m��
��B��m��0����OB=m
��OA=OB
���OAB=��OBA=45��
�ߡ�AFO=45������FAB+��FBA+��AFB=180��
���FAB=90��

��2������ͼ ����CP��AC �ֱ��� Rt��QPB�� Rt��QAB ��б���ϵ�����
��CP= ![]() ��
��![]() ��
��
��CP=AC=QC=BC
���CAB=��CBA
���CAB=��CBA=�������CBP=45��+��
���CPB=��CBP=45��+��
���PCB=180��-����CPB+��CBP��=90��-2��
�ߡ�ACB=180��-��CAB-��CBA=180��-2��
���ACP=��ACB-��PCB=180��-2��-��90��-2����=90��
��AC=CP
���ACP �ǵ���ֱ��������
���CPA=��CAP=45��
��CR��AP�����CRP=90������Rt��CRP��
sin��CPR![]()
��![]()
��![]() ��
��
��![]()
��![]()

��3������ A ��AH��CE �� EC ���ӳ����ڵ� H���ӳ� CH ���� G��ʹ HG=CH������AG
���AHC=��CEP=90��
���HAC+��HCA=��PCE+��HCA
���HAC=��PCE����AC=CP
���AHC�ա�CEP
��CH=PE=2��AH=CE����GH=CH=2��
![]()
��EG=CE+CH+GH=n+2+2=n+4
���DAP=�������AEG=2��
����+��=45��
�ߡ�EBD=��EDB=��HDA=��HAD=45��
���CAH=��HAD-��=45��-��=��
��AH ��ֱƽ�� GC
��AG=AC
���GAH=��CAH=��
���G=90��-�� �ڡ�EAG ��
��EAG=180��-��G-��AEG
=180��-��90��-����-2�� =90��-��
���EAG=��G
��EG=EA=n+4
�� Rt��AHE ��AE=HE+AH
![]()
![]() ���ᣩ
���ᣩ
��AH=OE=6��EP=EB=2
��OB=OE+BE=8
��m=8����A��0��8��
��OA=OF=8 �� ��F��-8��0��
��ֱ�� AF �Ľ���ʽΪ y x 8
��CD=CE-DE=CE-BE=6-2=4
���߶� CD ����ֱ�� AB �ĶԳ��߶� DS
��SD=CD=4����CDA=��SDA=45��
���CDS=90����
��SD��x ��
���� S �ֱ��� SM��x ���ڵ� M��SN��y ���ڵ� N
���ı��� OMSN��SMED ���Ǿ���
��OM=SN=OE-ME=2��ON=SM=DE=BE=2
��S(2��2)
��OP=OE-EP=6-2=4����P(4��0)
��ֱ�� PS �Ľ���ʽΪ y=ax+b
��![]() ����ã�
����ã�![]()
��ֱ�� PS�Ľ���ʽΪ y=-x+4
��ֱ��PS��ֱ��AF�Ľ���K(x��y)
��![]() ���
���![]()
��ֱ��PS��ֱ��AF�Ľ���K(-2��6)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
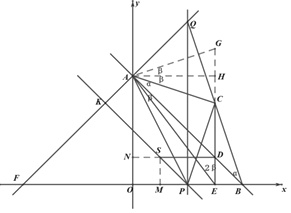
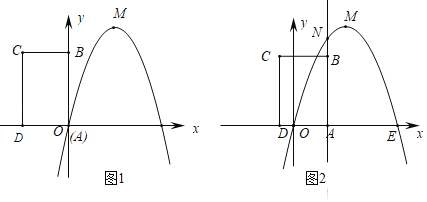
����Ŀ����ͼ����֪������y��x2��4��x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ��CΪ���㣬ֱ��y��x+m������A����y�ύ�ڵ�D��
��1�����߶�AD�ij���
��2����ֱ��AD����ƽ�Ƹ������ߵõ�һ�������ߣ����������ߵĶ���ΪC'������C'�ڷ���������![]() ��x��0����ͼ���ϣ����������߶�Ӧ�ĺ�������ʽ��
��x��0����ͼ���ϣ����������߶�Ӧ�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
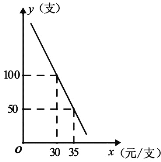
����Ŀ��ij����ר��һƷ�����࣬��ɱ�Ϊ22Ԫ/֧�������з��֣�����Ʒÿ���������![]() ��֧�������۵���
��֧�������۵���![]() ��Ԫ/֧��֮�������ͼ��ʾ�Ĺ�ϵ��
��Ԫ/֧��֮�������ͼ��ʾ�Ĺ�ϵ��
��1�������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����Ʒ���������۵��۶�Ϊ����Ԫʱ��ÿ���������������������Ƕ���Ԫ��
��3�����人����������״�����������ڼ䣬���������������ÿ���õ������г��100Ԫ�������人��Ϊ�˱�֤����ÿ��ʣ���������350Ԫ���ڿ�������״�����������ڼ䣬�г��ල�����ּӴ��˶����ϡ�������Ʒ���۵�ִ�����ȣ�����Ʒ�ۼ۳����ɱ��۵�20%���̼ҽ��д��������������������ṩһ�������������۵��۷�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����εı߳���Ϊ1���߶� AB�������˵����С�����εĶ����ϣ�
��1����ͼ�л�����ABΪֱ�DZߵ�Rt��ABC����C��С�����εĶ����ϣ���Rt��ABC�����Ϊ5��
��2���ڣ�1���������£�������BCD����D��С�����εĶ����ϣ���tan��CDB![]() ������AD����ֱ��д���߶�AD�ij���
������AD����ֱ��д���߶�AD�ij���
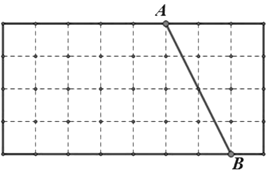
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��ͼ����A��B���㣮
��ͼ����A��B���㣮
��1������ͼ�е�����������������һ�κ����Ľ���ʽ��
��2�����AOB�������
��3������ͼ��ֱ��д��ʹһ�κ�����ֵ���ڷ�����������ֵ��x��ȡֵ��Χ��
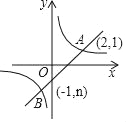
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾�������ԭ��![]() ��
��![]() ������һ��
������һ��![]() ������
������![]() ������Ϊ
������Ϊ![]() ������
������![]() �Ķ���
�Ķ���![]() ���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
��1���������������Ӧ�ĺ�����ϵʽ��
��2��������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶȴ�ͼ1��ʾ��λ����
����λ���ȵ��ٶȴ�ͼ1��ʾ��λ����![]() �������������ƽ���ƶ���ͬʱһ����
�������������ƽ���ƶ���ͬʱһ����![]() Ҳ����ͬ���ٶȴӵ�
Ҳ����ͬ���ٶȴӵ�![]() ������
������![]() �����ƶ����������˶���ʱ��Ϊ
�����ƶ����������˶���ʱ��Ϊ![]() ��
��![]() ��ֱ��
��ֱ��![]() ��������ߵĽ���Ϊ
��������ߵĽ���Ϊ![]() (��ͼ2��ʾ)��
(��ͼ2��ʾ)��
�ٵ�![]() ���жϵ�
���жϵ�![]() �Ƿ���ֱ��
�Ƿ���ֱ��![]() �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ�
����P��N��C��D��Ϊ����Ķ�������Ϊ![]() ������
������![]() �Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��б��BCΪһ������ABC��ͬ����������BCEF���������ε�����ΪO������AO�����AB=4��AO=6![]() ����ôAC=_____��
����ôAC=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ֻ�������Խ��Խ�ܵ����Ĺ�ע������һ���ڼ䣬�������������ijУ����������ѧ���ͼҳ�����ѧ�����ֻ�����Ŀ�����ͳ����������������������ͳ��ͼ��

![]() ����ε���ļҳ�����������ȫ����ͼ��
����ε���ļҳ�����������ȫ����ͼ��
![]() ������ͼ�б�ʾ�ҳ����ɡ���Բ�ĽǵĶ�����
������ͼ�б�ʾ�ҳ����ɡ���Բ�ĽǵĶ�����
![]() ��ij�������г���ѧ��
��ij�������г���ѧ��![]() �������������Щѧ���У�����ѧ�����ֻ�����֡�����ν��̬�ȵ�����Լ�Ƕ��٣�
�������������Щѧ���У�����ѧ�����ֻ�����֡�����ν��̬�ȵ�����Լ�Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com