
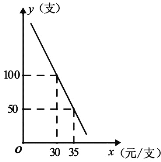
【题目】某网店专售一品牌牙膏,其成本为22元/支,销售中发现,该商品每天的销售量![]() (支)与销售单价
(支)与销售单价![]() (元/支)之间存在如图所示的关系.
(元/支)之间存在如图所示的关系.
(1)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该品牌牙膏销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)在武汉爆发“新型冠状病毒”疫情期间,该网店店主决定从每天获得的利润中抽出100元捐赠给武汉,为了保证捐款后每天剩余的利润不低于350元,在抗“新型冠状病毒”疫情期间,市场监督管理局加大了对线上、线下商品销售的执法力度,对商品售价超过成本价的20%的商家进行处罚,请你给该网店店主提供一个合理化的销售单价范围.
【答案】(1)![]() ;(2)销售单价定为31元时,每天最大利润为810元;(3)大于或等于25元小于或等于26.4元.
;(2)销售单价定为31元时,每天最大利润为810元;(3)大于或等于25元小于或等于26.4元.
【解析】
(1)由题图可知,![]() 与
与![]() 之间的函数经过点
之间的函数经过点![]() ,
,![]() ,设
,设![]() ,将两点坐标代入函数,然后求解即可;
,将两点坐标代入函数,然后求解即可;
(2)设每天的利润为![]() 元,则根据
元,则根据![]() ,然后将
,然后将![]() 代入,化简即可求解;
代入,化简即可求解;
(3)根据每日捐款100元,捐款后每天剩余的利润不低于350元,可得一元二次方程![]() ,利用二次函数的图像性质可求得
,利用二次函数的图像性质可求得![]() ,再根据商品售价不超过成本价的20%,可得不等式
,再根据商品售价不超过成本价的20%,可得不等式 ![]() ,求解即可得出解集.
,求解即可得出解集.
(1)解:据题意设![]()
将![]() ,
,![]() 代入得
代入得![]() ,
,
解之得![]()
∴![]() 与
与![]() 之间的关系式为
之间的关系式为![]()
(2)设每天的利润为![]() 元,则
元,则
![]()
![]()
![]()
∴销售单价定为31元时,每天最大利润为810元.
(3)![]() ,解得
,解得![]() 或37
或37
结合图像和二次函数的特点得出![]()
又![]() ,即:
,即:![]() ,
,
综合得![]()
∴按要求网店店主的销售单价范围为大于或等于25元小于或等于26.4元.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
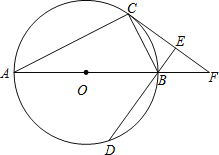
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:
①若AB=4,当OB=BF时,BE=______;
②当∠CAB的度数为______时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
(1)在直线l上任取一点B;
(2)以B为圆心,BA长为半径作弧,交直线l于点C;
(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;
(4)作直线AD.直线AD即为所求.

小云作图的依据是_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
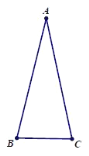
【题目】如图,![]() 中,
中,![]() .
.![]() . 将
. 将![]() 绕点
绕点![]() 顺时针旋转60°到点
顺时针旋转60°到点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,
,![]() .
.
(1)依题意补全图形:
(2)判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)请问在直线![]() 上是否存在点
上是否存在点![]() .使得
.使得![]() 恒成立若存在,请用文字描述出点
恒成立若存在,请用文字描述出点![]() 的准确位置,并画图证明;若不存在,请说明理由.
的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
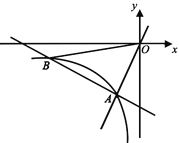
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的解析式;
(2)将直线![]() ,沿
,沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度得到的新直线
个单位长度得到的新直线![]() 与反比例函数
与反比例函数![]() 的图象只有一个公共点,求新直线
的图象只有一个公共点,求新直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
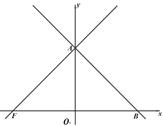
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线yx m交 y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
(1)求∠FAB的度数;
(2)点 P是线段OB上一点,过点P作 PQ⊥OB交直线 FA于点Q,连接 BQ,取 BQ的中点C,连接AP、AC、CP,过点C作 CR⊥AP于点R,设 BQ的长为d,CR的长为h,求d与 h的函数关系式(不要求写出自变量h的取值范围);
(3)在(2)的条件下,过点 C 作 CE⊥OB于点E,CE交 AB于点D,连接 AE,∠AEC=2∠DAP,EP=2,作线段 CD 关于直线AB的对称线段DS,求直线PS与直线 AF的交点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,P在BA的延长线上,C为圆上一点,且∠PCA=∠B.
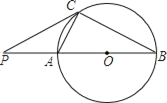
(1)求证:PC与⊙O相切;
(2)若PA=4,⊙O的半径为6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
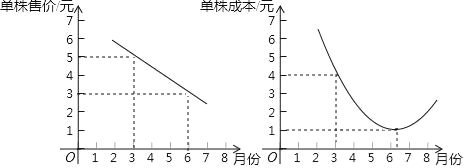
【题目】小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利多少元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大?(提示:单株获利=单株售价﹣单株成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com