
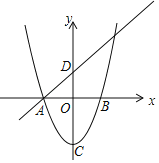
【题目】如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
(2)沿直线AD方向平移该抛物线得到一条新拋物线,设新抛物线的顶点为C',若点C'在反比例函数![]() (x<0)的图象上.求新抛物线对应的函数表达式.
(x<0)的图象上.求新抛物线对应的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)通过解方程求出点A的坐标,由此进一步求出![]() 的值,从而得出D点坐标,最后根据勾股定理计算即可;
的值,从而得出D点坐标,最后根据勾股定理计算即可;
(2)设新抛物线对应的函数表达式为![]() ,根据题意求出直线CC′的解析式,由此进一步求出C′坐标,据此再加以计算求解即可.
,根据题意求出直线CC′的解析式,由此进一步求出C′坐标,据此再加以计算求解即可.
(1)由![]() 得,
得,![]() ,
,![]() ,
,
∵点A位于点B的左侧,
∴A(![]() ,0),
,0),
∵直线![]() 经过点A,
经过点A,
∴![]() ,
,
∴m=2,
∴点D的坐标为(0,2),
∴AD=![]() ;
;
(2)设新抛物线对应的函数表达式为:![]() ,
,
∴C'(m,n),
∵CC′平行于直线AD,且经过C(0,4),
∴直线CC′的解析式为:![]() ,
,
∵点C'在反比例函数![]() (
(![]() )的图象上,
)的图象上,
∴![]() ,
,
∴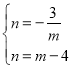 ,
,
解得:![]() 或
或![]() ,
,
∴新抛物线对应的函数表达式为![]() 或
或![]() ,
,
∴新抛物线对应的函数表达式为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
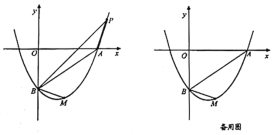
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
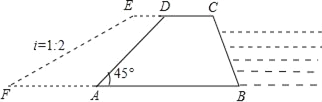
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
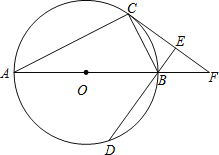
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:
①若AB=4,当OB=BF时,BE=______;
②当∠CAB的度数为______时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
(1)在直线l上任取一点B;
(2)以B为圆心,BA长为半径作弧,交直线l于点C;
(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;
(4)作直线AD.直线AD即为所求.

小云作图的依据是_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() .
.![]() . 将
. 将![]() 绕点
绕点![]() 顺时针旋转60°到点
顺时针旋转60°到点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,
,![]() .
.
(1)依题意补全图形:
(2)判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)请问在直线![]() 上是否存在点
上是否存在点![]() .使得
.使得![]() 恒成立若存在,请用文字描述出点
恒成立若存在,请用文字描述出点![]() 的准确位置,并画图证明;若不存在,请说明理由.
的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
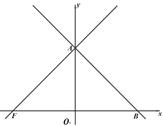
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线yx m交 y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
(1)求∠FAB的度数;
(2)点 P是线段OB上一点,过点P作 PQ⊥OB交直线 FA于点Q,连接 BQ,取 BQ的中点C,连接AP、AC、CP,过点C作 CR⊥AP于点R,设 BQ的长为d,CR的长为h,求d与 h的函数关系式(不要求写出自变量h的取值范围);
(3)在(2)的条件下,过点 C 作 CE⊥OB于点E,CE交 AB于点D,连接 AE,∠AEC=2∠DAP,EP=2,作线段 CD 关于直线AB的对称线段DS,求直线PS与直线 AF的交点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com