
【题目】已知,如图,在 ABC 中, ACB 90, B 60, BC 2 ,MON 30.
(1)如图 1, MON 的边 MO ⊥ AB ,边 ON 过点 C ,求 AO 的长;
(2)如图 2,将图 1 中的 MON 向右平移,MON 的两边分别与 ABC 的边 AC 、BC
相交于点 E 、 F ,连接 EF ,若 OEF 是直角三角形,求 AO 的长;
(3)在(2)的条件下,MON 与 ABC 重叠部分面积是否存在最大值,若存在,求出 最大值,若不存在,请说明理由.
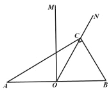
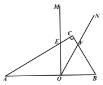
图 1 图 2 备用图
【答案】(1)2;(2) ![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先证△BOC是等边三角形,得BO=2,在![]() 中,
中,![]() ,
,![]() ,得AB=4.所以AO=AB-BO=2;
,得AB=4.所以AO=AB-BO=2;
(2)分两种情况①∠OEF=90°,设AO=![]() ,根据题意得
,根据题意得![]() ;②∠OFE=90°
;②∠OFE=90°
设AO=![]() ,根据题意得
,根据题意得![]() ;
;
(3)设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,根据题意得:
,根据题意得:![]() ,即
,即![]() ,求二次函数的最值可得.
,求二次函数的最值可得.
(1)∴∠MON=30°,MO⊥AB,
∴∠COB=60°,
∵∠B=60°,
∴△BOC是等边三角形,
∵BC=2,
∴BO=2,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴AB=4.
∴ AO=AB-BO=2.
(2)①∠OEF=90°
设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,![]() ,
,
∴![]() ∴
∴![]()
②∠OFE=90°
设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]() 是直角三角形时,AO长为
是直角三角形时,AO长为![]() 或
或![]()
(3)设AO=![]() ,根据题意得OB=
,根据题意得OB=![]() ,
,![]() ,
,
设重叠部分的面积为S,根据题意得:![]()
∴![]()
整理得:![]()
∵![]() ,
,
∴![]() 有最大值
有最大值
∴当![]() 时,
时,![]() 最大值
最大值![]()


科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费700元,乙工程队每天需工程费500元,甲工程队单独施工4天后由甲乙两个工程队共同完成余下的工程,则完成此项工程共需要多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 a 的正方形 ABCD 中, M 是边 AD 上一动点(点 M 与点 A 、 D 不重合), N 是 CD 的中点,且CBMNMB ,则 tan ABM (___________)
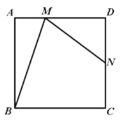
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
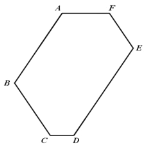
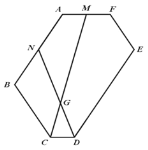
图 1 图 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】
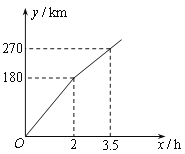
(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
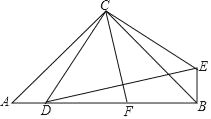
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
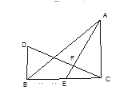
(1)求证.AE=CD;
(2)若BD=5㎝,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com