Question

20．如图1，数轴上，O点与C点对应的数分别是0、60（单位：单位长度），将一根质地均匀的直尺AB放在数轴上（A在B的左边），若将直尺在数轴上水平移动，当A点移动到B点的位置时，B点与C点重合，当B点移动到A点的位置时，A点与O点重合．
（1）直尺的长为20个单位长度（直接写答案）
（2）如图2，直尺AB在数轴上移动，有BC=4OA，求此时A点对应的数；
（3）如图3，以OC为边搭一个横截面为长方形的不透明的篷子，将直尺放入篷内的数轴上的某处（看不到直尺的任何部分，A在B的左边），将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动，直到完全看到直尺，所经历的时间为t₁、t₂，若t₁-t₂=2（秒），求直尺放入蓬内，A点对应的数为多少？

Answer 1

分析 （1）由题可知：OA=AB=BC，所以60÷3=20，则AB=20；
（2）有两种情况：利用图形直观得出，根据等量关系式BC=4OA，列式可求解；
（3）设A点对应的数为a（a＞0），向左移动所用的时间t₁=$\frac{20+a}{5}$，向右移动所用的时间t₂=$\frac{60-a}{5}$，根据t₁-t₂=2列式计算即可．

解答 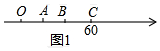解：（1）如图1，由题意得：OA=AB=BC，
∵OC=60，
∴AB=20，
故答案为：20；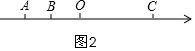
（2）由题意可知：直尺一定在C的左侧，
当AB在O的右侧时，如图2，
设点A表示的数为x（x＜0），
∵BC=4OA，
∴60-x-20=-4x，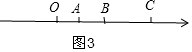
x=-$\frac{40}{3}$，
当AB在线段OC上时，如图3，
设点A表示的数为x（x＞0），则OA=x，BC=60-20-x，
由BC=4OA得：60-20-x=4x，
x=8，
综上所述，A点对应的数是-$\frac{40}{3}$或8；
（3）设A点对应的数为a（a＞0），
则$\frac{a+20}{5}-\frac{60-a}{5}$=2，
解得a=25，
答：A点对应的数为25．

点评 本题是数轴问题，与平移变换相结合，考查了数轴上表示的有理数与线段的长之间的关系；若点A表示的数为x_A，点B表示的数为x_B，则AB=|x_A-x_B|．