
分析 (1)(2)利用绝对值的意义直接求得答案即可;
(3)根据(2)的方法去绝对值,分为3种情况去绝对值符号,计算三种不同情况的值,最后讨论得出最小值.
解答 解:(1)|x|=3,
在数轴上与原点距离为3点的对应数为-3和3,
即x的值为-3和3.
(2)|x+2|=4,
在数轴上与-2的距离为4的点对应数为-6和2,
即x的值为2和--6.
(3)有最小值.最小值为3,
理由是:∵丨x-3丨+丨x-6丨理解为:在数轴上表示x到3和6的距离之和,
∴当x在3与6之间的线段上(即3≤x≤6)时:
即丨x-3丨+丨x-6丨的值有最小值,最小值为6-3=3.
点评 本题考查的是绝对值的性质及数轴的特点,根据题意能利用数形结合进行解答是解答此类问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.
已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
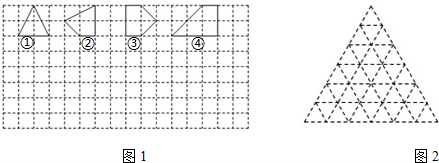
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
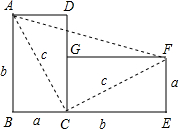 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
| n | 7 | 8 | 9 | 10 |
| m |
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com