
分析 设老师在黑板上要写的字大小为xcm×xcm,利用相似三角形的性质得$\frac{x•x}{0.42×0.42}$=($\frac{600}{30}$)2,然后解方程即可.
解答 解:设老师在黑板上要写的字大小为xcm×xcm时,才能使这名同学看黑板上的字时,与他看相距30cm的教科书上的字的感觉相同,
根据题意得$\frac{x•x}{0.42×0.42}$=($\frac{600}{30}$)2,
解得x=8.4.
答:老师在黑板上要写8.4cm×8.4cm的字,才能使这名同学看黑板上的字时,与他看相距30cm的教科书上的字的感觉相同.
点评 本题考查了相似三角形的性质:通常利用相似三角形的性质即相似三角形的对应边的比相等计算出被测量物的长度.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
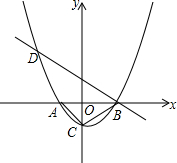 如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
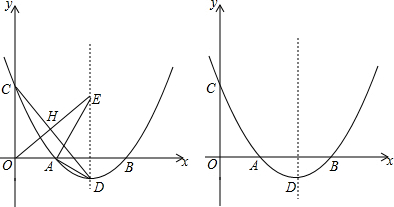
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
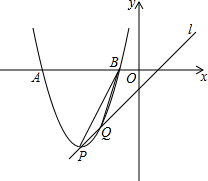 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com