
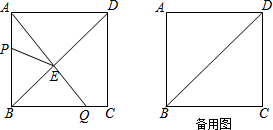
分析 (1)由正方形的性质和已知条件即可得出结果;
(2)由正方形的性质得出∠PBE=∠QBE,由AAS证明△BEP≌△BEQ,得出对应边相等BP=BQ,得出方程,解方程即可;
(3)分两种情况讨论:①当0<t≤2时;②当2<t<4时;由勾股定理得出方程,解方程即可.
解答 解:(1)PB=AB-AP,
∵AB=4,AP=1×t=t,
∴PB=4-t;
(2)t=$\frac{4}{3}$时,∠BEP和∠BEQ相等;理由如下:
∵四边形ABCD正方形,
∴对角线BD平分∠ABC,
∴∠PBE=∠QBE,
当∠BEP=∠BEQ时,
在△BEP与△BEQ中,$\left\{\begin{array}{l}{∠PBE=∠QBE}\\{∠BEP=∠BEQ}\\{BE=BE}\end{array}\right.$,
∴△BEP≌△BEQ(AAS),
∴BP=BQ,
即:4-t=2t,
解得:t=$\frac{4}{3}$;
(3)分两种情况讨论:
①当0<t≤2时;(即当P点在AB上,Q点在BC上运动时),
连接PQ,如图1所示: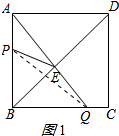
根据勾股定理得:$B{P^2}+B{Q^2}={(2\sqrt{5})^2}$,
即(4-t)2+(2t)2=(2$\sqrt{5}$)2,
解得:t=2或t=-$\frac{2}{5}$(负值舍去);
②当2<t<4时,(即当P点在AB上,Q点在CD上运动时),
作PM⊥CD于M,
如图2所示: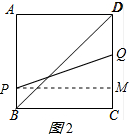 则PM=BC=4,CM=BP=4-t,
则PM=BC=4,CM=BP=4-t,
∴MQ=2t-4-(4-t)=3t-8,
根据勾股定理得:MQ2+PM2=PQ2,
即${(3t-8)^2}+{4^2}={(2\sqrt{5})^2}$,
解得t=$\frac{10}{3}$或t=2(舍去);
综上述:当t=2或$\frac{10}{3}$时;PQ之间的距离为2$\sqrt{5}$cm.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、解方程等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,根据勾股定理得出方程,解方程才能得出结果.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
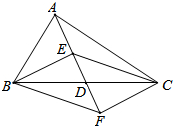 如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是③(只填写序号).
如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是③(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
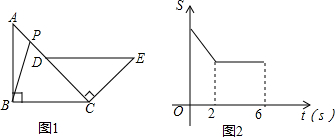
| A. | 2+$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
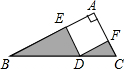 如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
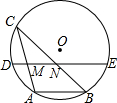 如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.
如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com