
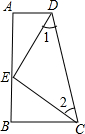
 如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则:
如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则:分析 (1)利用“HL”证明Rt△ADE≌Rt△BEC.
(2)△DEC是等腰直角三角形,证明∠DEC=90°,即可解答;
(3)利用在直角三角形中,斜边的中线等于斜边的一半,即可解答.
解答 解:(1)∵∠1=∠2,
∴DE=CE,
∵DA⊥AB于点A,CB⊥AB于点B,
∴∠A=∠B=90°,
在Rt△DAE和Rt△EBC中,
$\left\{\begin{array}{l}{DE=CE}\\{AE=BC}\end{array}\right.$
∴Rt△DAE≌Rt△EBC.
(2)△DEC是等腰直角三角形,
∵Rt△DAE≌Rt△EBC.
∴∠ADE=∠BEC,
∵∠ADE+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=180°-(∠BEC+∠AED)=90°,
∵∠1=∠2,
∴DE=CD,
∴△DEC是等腰直角三角形.
(3)如图,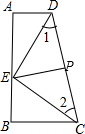
∵△DEC是等腰直角三角形.CD=10,P是CD的中点,
∴PE=$\frac{1}{2}$CD=$\frac{1}{2}×10$=5(在直角三角形中,斜边的中线等于斜边的一半).
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明Rt△ADE≌Rt△BEC.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{πx}{5}$的系数是$\frac{1}{5}$ | B. | $\frac{3x-1}{3}$是单项式 | ||
| C. | -25m是5次单项式 | D. | -x2y-35xy3是四次多项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量(x台) | 每台奖励金额(元) |
| 0<x≤100 | 200 |
| 100<x≤300 | 500 |
| x>300 | 1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
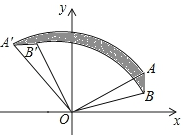 如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,B旋转到点B′位置.
如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,B旋转到点B′位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com