
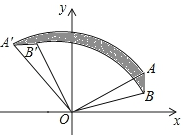
 如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,B旋转到点B′位置.
如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2$\sqrt{3}$)的位置,B旋转到点B′位置.分析 (1)由A(2$\sqrt{3}$,2)旋转到点A′(-2,2$\sqrt{3}$),易得旋转角为90°,根据逆时针旋转90°后点的横坐标等于旋转前点的纵坐标的相反数,纵坐标等于旋转前点的横坐标可得出B′的坐标;
(2)根据旋转的性质可得,阴影部分的面积等于S扇形A'OA-S扇形C'OC,从而根据A,B点坐标知OA=4,OC=OB=$\sqrt{13}$,可得出阴影部分的面积.
解答 解:(1)∵将△AOB绕着点O逆时针旋转,使点A(2$\sqrt{3}$,2)旋转到点A′(-2,2$\sqrt{3}$)的位置,B旋转到点B′位置,
∴∠A′OA=∠B′OB=90°,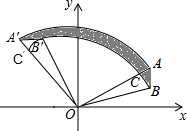 ∵B(2$\sqrt{3}$,1),
∵B(2$\sqrt{3}$,1),
∴B′点坐标为(-1,2$\sqrt{3}$);
(2)如图,设$\widehat{BB′}$与OA交于点C,与OA′交于点C′,
∵A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),
∴OA=4,OC=OB=$\sqrt{13}$.
根据旋转的性质可得,SOB′C′=SOBC,
∴阴影部分的面积=S扇形A'OA-S扇形C'OC=$\frac{1}{4}$π×42-$\frac{1}{4}$π×($\sqrt{13}$)2=$\frac{3}{4}$π.
点评 此题主要考查了扇形的面积计算及旋转的性质,解答本题的关键是根据旋转的性质得出SOB′C′=SOBC,从而得到阴影部分的表达式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
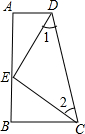 如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则:
如图,DA⊥AB于点A,CB⊥AB于点B,E是AB上一点,且BC=AE,∠1=∠2,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.
小明家离学校5千米,放学后,爸爸从家里出发去学校接小明,与此同时小明从学校出发往家走,已知爸爸的速度是6千米/小时,小明的速度是4千米/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com