
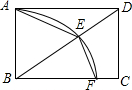
 如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
分析 由矩形的性质得出∠BAD=∠ABC=90°,由等腰三角形的性质得出∠BFE=∠BEF=70°,∠BAE=∠BEA,由三角形内角和定理求出∠EBF=40°,由角的互余关系求出∠ABE,再由三角形内角和定理求出∠BAE的度数,即可得出∠DAE的度数.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,
∵BE=BF=BA,
∴∠BFE=∠BEF=70°,∠BAE=∠BEA,
∴∠EBF=180°-70°-70°=40°,
∴∠ABE=90°-40°=50°,
∴∠BAE=∠BEA=(180°-50°)÷2=65°,
∴∠DAE=90°-65°=25°;
故选:C.
点评 本题考查了矩形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握矩形和等腰三角形的性质,求出∠BAE是解决问题的突破口.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抽取的200名学生的期末考试成绩的极差是60分 | |
| B. | 总体是抽取的200名学生的期末考试成绩 | |
| C. | 样本容量是200 | |
| D. | 个体是每个九年级学生的期末考试成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
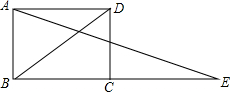 如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )
如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com