
【题目】如图,P 是等边三角形 ABC 内的一点,连接 PA、PB、PC,以 BP 为边作∠PBQ=60°,且 BQ=BP,连接 CQ.
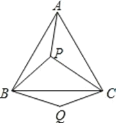
(1)观察并猜想 AP 与 CQ 之间的大小关系,并说明理由.
(2)若 PA=3,PB=4,PC=5,∠BQC= .(请直接写出∠BQC 的度数)
【答案】(1)AP=CQ,理由见解析;(2)150°
【解析】
(1)根据“SAS”证明△ABP≌△CBQ,可得AP=CQ;
(2)连接PQ.证明△PBQ为等边三角形,得∠PQB=60°;根据三边长度可证△PQC为直角三角形,得∠PQC=90°.
解:(1)AP=CQ,理由如下:
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°.
∵∠PBQ=60°,
∴∠ABP=∠CBQ=60°-∠PBC.
在△ABP和△CBQ中,
 ,
,
∴△ABP≌△CBQ,
∴AP=CQ;
(2)连接PQ.

∵BP=BQ,∠PBQ=60°,
∴△PBQ是等边三角形,
∴∠PQB=60°,PQ=PB=4.
又∵CQ=PA=3,PC=5,52=32+42,即PC2=PQ2+CQ2,
∴△PQC是直角三角形,且∠PQC=90°,
∴∠BQC=60°+90°=150°.


科目:初中数学 来源: 题型:
【题目】为了对某市区全民阅读状况进行调查和评估,有关部门随机抽取了部分市民进行每天阅读时间情况的调查,并根据调查结果制做了如下尚不完整的频数分布表(被调查者每天的阅读时间均在0﹣120分钟之内)
阅读时间x(分钟) | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x≤120 |
频数 | 450 | 400 | m | 50 |
频率 | 0.45 | 0.4 | 0.1 | n |
(1)被调查的市民人数为多少,表格中,m,n为多少;
(2)补全频数分布直方图;
(3)某市区目前的常住人口约有118万人,请估计该市区每天阅读时间在60~120分钟的市民大约有多少万人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段![]() 、
、![]() 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程![]() (米)与所用时间
(米)与所用时间![]() (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
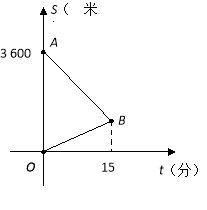
【1】求点![]() 的坐标和
的坐标和![]() 所在直线的函数关系式
所在直线的函数关系式
【2】小明能否在比赛开始前到达体育馆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:如图①,在四边形ABCD中,AB=AD,∠ABC=∠ADC,那么BC=CD吗?请说明理由.

小明的作法如下:
如图②,连结AC.
∵AB=AD,∠ABC=∠ADC,AC=AC.
∴△ABC≌△ADC.
∴BC=CD.
(1)小明的作法错误的原因是 .
(2)请正确解答这道题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于点A(2,0),与反比例函数y=![]() 的图象交于点B(3,n).
的图象交于点B(3,n).
(1)求一次函数与反比例函数的表达式;
(2)若点P为x轴上的点,且△PAB的面积是2,则点P的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)四面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y与S的函数关系式;
(2)求当面条粗1.6 mm2时,面条的总长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
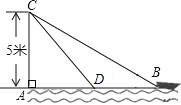
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t
(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了30分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有320米
其中正确的结论有( )

A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
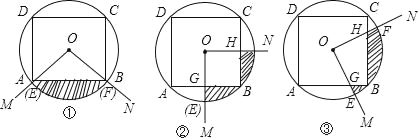
【题目】如图,正方形ABCD内接于⊙O,圆心O是正方形的对称中心,⊙O的面积为S1,正方形的面积为S2,则以圆心O为顶点,作∠MON=90°,将∠MON绕O点旋转,OM、ON分别与⊙O交于E、F,分别于正方形ABCD交于G、H,设由OE、OF、EF及正方形ABCD的边围成的图形(阴影部分)的面积为S,那么:
(1)如图①,当OM经过点A时,S、S1、S2之间的关系(用S1、S2的代数式表示S)为 ;
(2)如图②,当OM⊥AB交于点G时,①中的结论还成立吗?并说明理由;
(3)如图③,∠MON旋转到任意位置时,则①中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com