
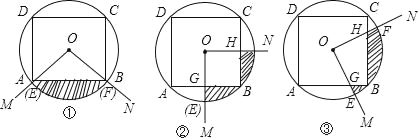
【题目】如图,正方形ABCD内接于⊙O,圆心O是正方形的对称中心,⊙O的面积为S1,正方形的面积为S2,则以圆心O为顶点,作∠MON=90°,将∠MON绕O点旋转,OM、ON分别与⊙O交于E、F,分别于正方形ABCD交于G、H,设由OE、OF、EF及正方形ABCD的边围成的图形(阴影部分)的面积为S,那么:
(1)如图①,当OM经过点A时,S、S1、S2之间的关系(用S1、S2的代数式表示S)为 ;
(2)如图②,当OM⊥AB交于点G时,①中的结论还成立吗?并说明理由;
(3)如图③,∠MON旋转到任意位置时,则①中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)![]() ;(2)成立;(3)成立.
;(2)成立;(3)成立.
【解析】
(1)如图①,利用正方形的性质得到∠AOB=90°,则可判断OM经过点A时,ON经过点B,根据扇形的面积公式,利用S=S扇形EOF﹣S△AOB得到S=![]() (S1﹣S2);
(S1﹣S2);
(2)如图②,先证明ON⊥BC,利用S=S扇形EOF﹣S矩形OGBH得到S=![]() (S1﹣S2),从而判断(1)的结论成立;
(S1﹣S2),从而判断(1)的结论成立;
(3)如图③,连接OB、OA,先证明∠AOE=∠BOH,则判断△AOG≌△BOH,从而得到S△AOG=S△BOH,所以S四边形OGBH=S△AOB,然后利用S=S扇形EOF﹣S四边形OGBH=S扇形EOF﹣S△AOB得到S=![]() (S1﹣S2),于是可判断(1)中的结论成立.
(S1﹣S2),于是可判断(1)中的结论成立.
(1)如图①.
∵正方形ABCD内接于⊙O,圆心O是正方形的对称中心,∴∠AOB=90°.
∵∠MON=90°,∴OM经过点A时,ON经过点B,∴S=S扇形EOF﹣S△AOB=![]() S1﹣
S1﹣![]() S2=
S2=![]() (S1﹣S2).
(S1﹣S2).
故答案为:![]() (S1﹣S2);
(S1﹣S2);
(2)成立.理由如下:
如图②,当OM⊥AB交于点G时.
∵∠ABC=90°,∠GOH=90°,∴∠OHB=90°,∴ON⊥BC,∴S=S扇形EOF﹣S矩形OGBH=![]() S1﹣
S1﹣![]() S2=
S2=![]() (S1﹣S2);
(S1﹣S2);
(3)成立.理由如下:
如图③,连接OB、OA.
∵四边形ABCD为正方形,∴OA=OB,∠OAB=∠OBC=45°.
∵∠AOB=90°,∠EOF=90°,∴∠AOE=∠BOH.在△AOG和△BOH中,∵
 ,∴△AOG≌△BOH,∴S△AOG=S△BOH,∴S四边形OGBH=S△AOB,∴S=S扇形EOF﹣S四边形OGBH=S扇形EOF﹣S△AOB=
,∴△AOG≌△BOH,∴S△AOG=S△BOH,∴S四边形OGBH=S△AOB,∴S=S扇形EOF﹣S四边形OGBH=S扇形EOF﹣S△AOB=![]() S1﹣
S1﹣![]() S2=
S2=![]() (S1﹣S2).
(S1﹣S2).


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,P 是等边三角形 ABC 内的一点,连接 PA、PB、PC,以 BP 为边作∠PBQ=60°,且 BQ=BP,连接 CQ.
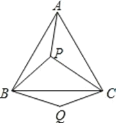
(1)观察并猜想 AP 与 CQ 之间的大小关系,并说明理由.
(2)若 PA=3,PB=4,PC=5,∠BQC= .(请直接写出∠BQC 的度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
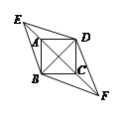
【题目】如图,正方形ABCD的边长为3![]() ,对角线AC、BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为( )
,对角线AC、BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为( )
A. 20B. 24C. 12![]() D. 12
D. 12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
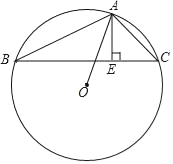
【题目】如图,在钝角△ABC中,∠C=45°,AE⊥BC,垂足为E点,且AB与AC的长度为方程x2﹣9x+18=0的两个根,⊙O是△ABC的外接圆.
求:(1)⊙O的半径;
(2)BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
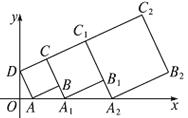
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2017个正方形的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
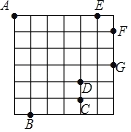
A.点A、点B、点CB.点A、点D、点G
C.点B、点E、点FD.点B、点G、点E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式![]() ,
,![]() 是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式
是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式![]() ,
,![]() 是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,
是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,![]() .
.
(1)将假分式![]() 化为一个整式与一个真分式的和是 ;
化为一个整式与一个真分式的和是 ;
(2)将假分式![]() 化为一个整式与一个真分式的和;
化为一个整式与一个真分式的和;
(3)若分式![]() 的值为整数,求整数x的值.
的值为整数,求整数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com