
【题目】如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
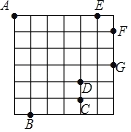
A.点A、点B、点CB.点A、点D、点G
C.点B、点E、点FD.点B、点G、点E
【答案】C
【解析】
先利用勾股定理求出各边的长,再利用勾股定理的逆定理:如果三边满足![]() ,则可组成直角三角形进行判断即可.
,则可组成直角三角形进行判断即可.
A.AB2=1+36=37,AC2=16+25=41,BC2=1+9=10,37+10≠41,不可以构成直角三角形;
B.AD2=16+16=32,AG2=9+36=45,DG2=1+4=5,32+5≠45,不可以构成直角三角形;
C.BE2=36+16=52,BF2=25+25=50,EF2=1+1=2,50+2=52,可以构成直角三角形
D.BG2=25+9=34,BE2=36+16=52,GE2=9+1=10,34+10≠52,不可以构成直角三角形.
故选:C.


科目:初中数学 来源: 题型:
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
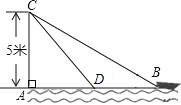
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
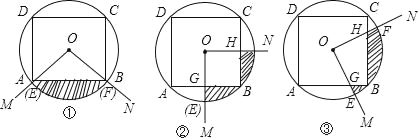
【题目】如图,正方形ABCD内接于⊙O,圆心O是正方形的对称中心,⊙O的面积为S1,正方形的面积为S2,则以圆心O为顶点,作∠MON=90°,将∠MON绕O点旋转,OM、ON分别与⊙O交于E、F,分别于正方形ABCD交于G、H,设由OE、OF、EF及正方形ABCD的边围成的图形(阴影部分)的面积为S,那么:
(1)如图①,当OM经过点A时,S、S1、S2之间的关系(用S1、S2的代数式表示S)为 ;
(2)如图②,当OM⊥AB交于点G时,①中的结论还成立吗?并说明理由;
(3)如图③,∠MON旋转到任意位置时,则①中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
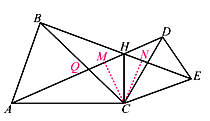
【题目】如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE交于点H,连接CH.
(1)求证:△ACD≌△BCE;
(2)求证:CH平分∠AHE;
(3)求∠CHE的度数.(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③(x﹣2)(x+5)=x2﹣1;④3x2﹣![]() =0.
=0.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com