
【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.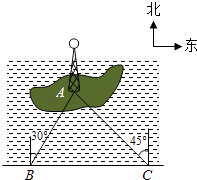
【答案】解:过A作AD⊥BC于D,则AD的长度就是A到岸边BC的最短距离.
在Rt△ACD中,∠ACD=45°,设AD=x,则CD=AD=x,
在Rt△ABD中,∠ABD=60°,
由tan∠ABD= ![]() ,即tan60°=
,即tan60°= ![]() ,
,
所以BD= ![]() =
= ![]() x,
x,
又BC=4,即BD+CD=4,所以 ![]() x+x=4,
x+x=4,
解得x=6﹣2 ![]() .
.
答:这个标志性建筑物底部A到岸边BC的最短距离为(6﹣2 ![]() )公里.
)公里.
【解析】过A作AD⊥BC于D,先由△ACD是等腰直角三角形,设AD=x,得出CD=AD=x,再解Rt△ABD,得出BD= ![]() =
= ![]() x,再由BD+CD=4,得出方程
x,再由BD+CD=4,得出方程 ![]() x+x=4,解方程求出x的值,即为A到岸边BC的最短距离.
x+x=4,解方程求出x的值,即为A到岸边BC的最短距离.
【考点精析】掌握等腰直角三角形是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2![]() , 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
, 且AB、AE的长是关于x的方程x2﹣8x+k=0的两个实数根.
(1)求⊙O的半径.
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.

(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)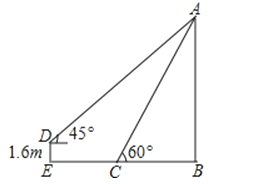
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣ ![]() ,0),且与反比例函数y=
,0),且与反比例函数y= ![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B. 
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,点N的距离相等,那么x的值是______________;
(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
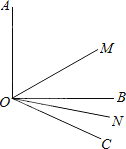
【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com