
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]()
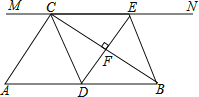
(1)当![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(2)当![]() 为
为![]() 中点时,
中点时,![]() 等于 度时,四边形
等于 度时,四边形![]() 是正方形.
是正方形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣![]() x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
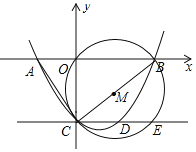
(1)求该抛物线的解析式;
(2)当△PDE是以DE为底边的等腰三角形时,求点P的坐标;
(3)当四边形ACPB的面积最大时,求点P的坐标并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
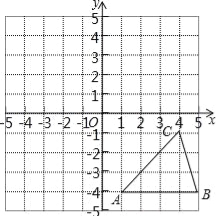
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)作出△ABC关于y轴对称的![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的![]() ,并求出
,并求出![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
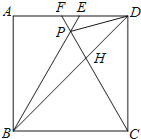
【题目】如图,在正方形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() 、
、![]() 的延长线分别交
的延长线分别交![]() 于点
于点![]() 、
、![]() ,连结
,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .给出下列结论:①
.给出下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 其中正确结论的序号是( )
其中正确结论的序号是( )
A.①②B.②③④C.①③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
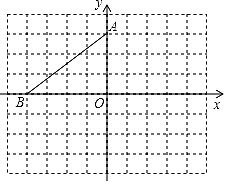
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(0,3)、(-4,0).
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O、B对应点分别是E、F,请在图中面出△AEF;
(2)以点O为位似中心,将三角形AEF作位似变换且缩小为原来的![]() 在网格内画出一个符合条件的
在网格内画出一个符合条件的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 所在的直线交
所在的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() . 下列结论中,正确的有_________ (填序号).
. 下列结论中,正确的有_________ (填序号).
①![]() ;②
;②![]() 是
是![]() 的一个三等分点;③
的一个三等分点;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+2x+3交x轴于点A、B,其中点A在点B的左边,交y轴于点C,点P为抛物线上位于x轴上方的一点.
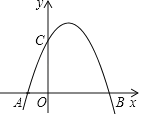
(1)求A、B、C三点的坐标;
(2)若△PAB的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com