
����Ŀ��ijУ��չ���ԡ��������ģ��μ�ʹ����Ϊ�����֪ʶ�������ִӸ�У�ˡ����꼶�������ȡ10��ѧ���ijɼ����������������ͷ������ɼ���m��ʾ�������ֳ��ĸ��飺A.80��m��85��B.85��m��90��C.90��m��95��D.95��m��100����������˲�����Ϣ���£�
���꼶10��ѧ���ijɼ���99��80��99��86��99��96��90��100��89��82��
���꼶10��ѧ���ijɼ���C������ݣ�94��90��94��
�ˡ����꼶��ȡѧ���ɼ�ͳ�Ʊ� | ||
�꼶 | ���꼶 | ���꼶 |
ƽ���� | 92 | 92 |
��� | 93 | b |
���� | c | 100 |
���� | 52 | 50.4 |
����������Ϣ������������⣺
��1������ͼ���е�a���� ����b���� ����c���� ����
��2������ͳ��ͼ�С�D�顱����Ӧ��Բ�ĽǵĶ���Ϊ�� ����
��3������������Ϣ������Ϊ�ĸ��꼶��ѧ���ԡ��������ģ��μ�ʹ�������������սϺã�˵�����ɣ���һ�����ɣ�
��4����У���꼶����840��ѧ���μ���֪ʶ����������ƾ��꼶�μӴ˴�֪ʶ������ɼ�Ϊ�Ϻã�90��m��95����ѧ���ж����ˣ�

���𰸡���1��40��b��94��c��99����2��144�㣻��3�����꼶�����������������4��252
��������
��1�����������ͳ��ͼ�е����ݡ������е����ݿ��Էֱ�õ�a��b��c��ֵ��
��2����������ͳ��ͼ�е����ݿ��Եõ�����ͳ��ͼ����D��������Ӧ��Բ�ĽǵĶ�����
��3�����ݱ����е����ݣ����Խ���⣬ע������д��һ�����ɣ�
��4������ͳ��ͼ�е����ݿ��Լ�������꼶�μӴ˴�֪ʶ������ɼ�Ϊ�Ϻã�90��m��95����ѧ���ж����ˣ�
�⣺��1���߾��꼶10��ѧ���ijɼ���C������ݣ�94��90��94��
��C��ռ�İٷֱ�Ϊ��3��10��100%��30%��
��a%��1��20%��10%��30%��40%��
��a��ֵΪ40��
b��94��
c��99��
�ʴ�Ϊ��40��94��99��
��2������ͳ��ͼ����D��������Ӧ��Բ�ĽǵĶ���Ϊ360���40%��144����
�ʴ�Ϊ��144����
��3�����꼶��ѧ�������������ģ��μ�ʹ�������������սϺã�
���ɣ����꼶����λ�����ڰ��꼶����λ����˵�����꼶�ijɼ����ڰ��꼶��
��4��840��30%��252���ˣ���
�𣺾��꼶�μӴ˴�֪ʶ������ɼ�Ϊ�Ϻã�90��m��95����ѧ����252�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
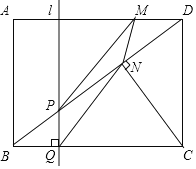
����Ŀ����ͼ���ھ���ABCD�У�CD��3cm��BC��4cm������BD��������C��CN��BD������ΪN��ֱ��l��ֱBC���ֱ�BD��BC�ڵ�P��Q��ֱ��l��AB��������ÿ��1cm���ٶ���BC���������˶���CDΪֹ����M���߶�DA��ÿ��1cm���ٶ��ɵ�D���A�����˶�������AΪֹ��ֱ��1���Mͬʱ���������˶�ʱ��Ϊt�루t��0����
��1���߶�CN���� ����
��2������PM��QN�����ı���MPQNΪƽ���ı���ʱ����t��ֵ��
��3���������˶������У���tΪ��ֵʱ��PMN�����ȡ�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABΪֱ���ġ�O����BAD��ƽ�����ڵ�C����AD�ڵ�F������C��CD��AD��D����AB���ӳ����ڵ�E��
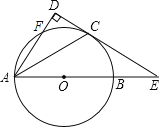
��1����֤��CDΪ��O�����ߣ�
��2����![]() ��
��![]() ����cos��DAB��ֵ��
����cos��DAB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��1����λ���ٶ����յ�
��ÿ��1����λ���ٶ����յ�![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��2����λ���ٶ����յ�
��ÿ��2����λ���ٶ����յ�![]() �˶�����
�˶�����![]() ��
��![]() ��������һ�㵽���
��������һ�㵽���![]() ʱ����һ��Ҳ��ֹ֮ͣ�˶�������
ʱ����һ��Ҳ��ֹ֮ͣ�˶�������![]() ��
��![]() ������
������![]() ��
��![]() ������
������![]() ���
���![]() ���غ�ʱ����
���غ�ʱ����![]() ��
��![]() Ϊ�ڱ���
Ϊ�ڱ���![]() ����
����![]() ��
��![]() ������˶�ʱ��Ϊ
������˶�ʱ��Ϊ![]() �룮
�룮
��1�����߶�![]() �ij���(�ú�
�ij���(�ú�![]() �Ĵ���ʽ��ʾ)
�Ĵ���ʽ��ʾ)
��2����![]() �ڱ�
�ڱ�![]() ���˶�������
���˶�������![]() ���ڱ�
���ڱ�![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ������
������![]() ��
��![]() �ڲ�ʱ����
�ڲ�ʱ����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4����![]() ��һ�������ڱ�2��ʱ��ֱ��д��
��һ�������ڱ�2��ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
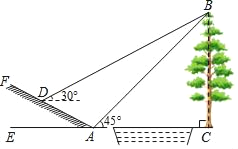
����Ŀ����ͼ��ʾ��ij��ѧ�С��ѡ������С�Ӷ�����BC�ĸ߶ȣ�������б��AF�ϵ�D����ô�������B��������30�㣬�ڵ�����A����ô�������B��������45�㣮���½ǡ�FAE��30�㣬AD��6m��������ĸ߶ȣ�(��������������ο����ݣ�![]() ��1.73)
��1.73)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ����
����![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣨��
��һ���㣨��![]() �����
�����![]() �غϣ�����
�غϣ�����![]() Ϊ��������ֱ��
Ϊ��������ֱ��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��
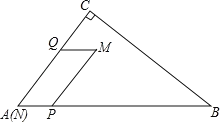
��1���۲����
��ͼ1������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
��![]() ��
��![]() ��λ�ù�ϵΪ__________��
��λ�ù�ϵΪ__________��
��![]() ֮���������ϵΪ___________����ʾ����֤
֮���������ϵΪ___________����ʾ����֤![]() ��
��

��2����ѧ˼��
��ͼ2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����1���еĢ١��ڽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
���ӳ�����ʱ����1���еĢ١��ڽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
��3����չ����
��ͼ3������![]() ���߶�
���߶�![]() ���ӳ���ʱ����
���ӳ���ʱ����![]() ���߶�
���߶�![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() ���
���![]() �غϣ�����
�غϣ�����![]() ����
����![]() ����ֱ��д���߶�
����ֱ��д���߶�![]() �ij�������ʾ����
�ij�������ʾ����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��ƿ��ͬŨ�ȵľƾ���Aƿ���оƾ�2kg��Ũ��x%��Bƿ�оƾ�3kg��Ũ��y%��Cƿ�оƾ�5kg��Ũ��z%����Aƿ�е���10%��Bƿ�е���20%��Cƿ�е���24%����Ϻ���Ũ��33.5%������Ϻ����Һ����ƿ�У�ʹ���ǻָ�ԭ�����������ٴ�Aƿ����30%��Bƿ����30%��Cƿ����30%����Ϻ���Ũ��Ϊ31.5%����������![]() ��
��![]() ��
��![]() ����x��y��z��Ϊ������������A��B��ƿ�ƾ�ȫ����Ϻ��Ũ��Ϊ______��
����x��y��z��Ϊ������������A��B��ƿ�ƾ�ȫ����Ϻ��Ũ��Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ����У�װ�г���ɫ���������ͬ�ĺ졢����������֪���к�����3�����Ҵ�����������һ���Ǻ���ĸ���Ϊ0.75.
��1���������⣬������ ������.
��2������һ���������һ���Żأ�����������ڶ�����.���û���״ͼ���б�������������������һ����Ϊ����Ϊ�¼�A�����ĸ���P��A��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����x2+��m��2��x+3��m+1����x�ύ��AB���㣨A��B��ࣩ����y�������ύ�ڵ�C��
��1����m�٩�4ʱ��˵��������κ�����ͼ����x������������㣻
��2����OAOB��6�����C�����ꣻ
��3���ڣ�2���������£���x���·�������������һ��P��ʹS��PAC�����Ϊ15����P������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com