
【题目】如图,以AB为直径的⊙O交∠BAD的平分线于点C,交AD于点F,过点C作CD⊥AD于D,交AB的延长线于点E.
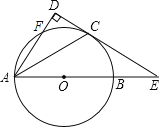
(1)求证:CD为⊙O的切线;
(2)若![]() =
=![]() ,求cos∠DAB的值.
,求cos∠DAB的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,如图,证明∠DAC=∠OCA得到AD∥OC,再利用平行线的性质得到OC⊥DE,然后根据切线的判定定理得到结论;
(2)作OH⊥AD于H,如图,则AH=HF,由四边形OCDH为矩形得到OH=CD,OC=DH,设CD=x,⊙O的半径为r,则AH=2x-r,OA=r,在Rt△OAH中利用勾股定理得到x2+(2x-r)2=r2,解得x=![]() r,然后利用余弦定义求解.
r,然后利用余弦定义求解.
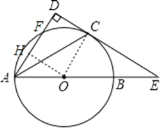
(1)证明:连接OC,如图,
∵AC平分∠BAD,
∴∠DAC=∠EAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴CD为⊙O的切线;
(2)作OH⊥AD于H,如图,则AH=HF,
易得四边形OCDH为矩形,
∴OH=CD,OC=DH,
∵![]() =
=![]() ,
,
∴设CD=x,则AD=2x,
设⊙O的半径为r,
∴AH=2x﹣r,OA=r,
在Rt△OAH中,x2+(2x﹣r)2=r2,解得x=![]() r,
r,
∴AH=![]() r,
r,
在Rt△OAH中,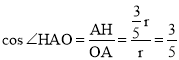 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某超市促销活动,将A,B,C三种水果采用甲、乙、丙三种方式搭配装进礼盒进行销售.每盒的总成本为盒中A,B,C三种水果成本之和,盒子成本忽略不计.甲种方式每盒分别装A,B,C三种水果6kg,3kg,1kg;乙种方式每盒分别装A,B,C三种水果2kg,6kg,2kg.甲每盒的总成本是每千克A水果成本的12.5倍,每盒甲的销售利润率为20%;每盒甲比每盒乙的售价低25%;每盒丙在成本上提高40%标价后打八折出售,获利为每千克A水果成本的1.2倍.当销售甲、乙、丙三种方式搭配的礼盒数量之比为2:2:5时,则销售总利润率为_____.(利润率=利润÷成本×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的![]() ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的
,乙型车辆是丙型车数量的2倍,上午安排甲车数量的![]() ,乙车数量的
,乙车数量的![]() ,丙车数量的
,丙车数量的![]() 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的
进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的![]() ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的
;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的![]() .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为_____元.
.已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
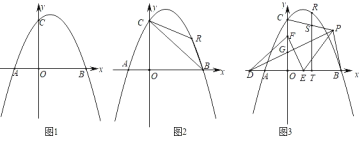
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.

小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
如图,![]() 内接于
内接于![]() ,直径
,直径![]() 的长为2,过点
的长为2,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
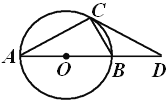
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:
小明:我加的条件是![]() ,就可以求出
,就可以求出![]() 的长
的长
小聪:你这样太简单了,我加的是![]() ,连结
,连结![]() ,就可以证明
,就可以证明![]() 与
与![]() 全等.
全等.
参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
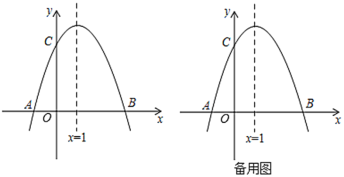
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外给出了部分信息如下:
八年级10名学生的成绩:99,80,99,86,99,96,90,100,89,82.
九年级10名学生的成绩在C组的数据:94,90,94.
八、九年级抽取学生成绩统计表 | ||
年级 | 八年级 | 九年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)上面图表中的a= ,b= ,c= .
(2)扇形统计图中“D组”所对应的圆心角的度数为 .
(3)根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好?说明理由.(一条即可)
(4)该校九年级共有840名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好(90≤m<95)的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
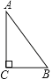
【题目】如图,在△ABC 中,∠C=90°,AB=10cm,BC=6cm,动点 P 从点 C 出发,沿 C﹣A﹣B﹣C 运动,速度为 2cm/s,动点 Q 从点 C 出发,沿 C﹣B﹣A﹣C 运动,速度为![]() cm/s,两点相遇时停止.这一过程中 P,Q 两点之间的距离 y 与时间 t 之间的关系的大致图象是( )
cm/s,两点相遇时停止.这一过程中 P,Q 两点之间的距离 y 与时间 t 之间的关系的大致图象是( )
A.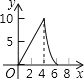 B.
B.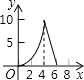 C.
C.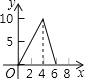 D.
D.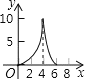
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com