
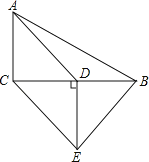
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.
【答案】(1)详见解析;(2)10+2![]() .
.
【解析】
试题由已知易证AC∥DE,又CE∥AD,所以四边形ACED是平行四边形;
(2)四边形ACED是平行四边形,可得DE=AC=2.在Rt△CDE中,由勾股定理得CD=2![]() ,再由D是BC的中点可得BC=2CD=4
,再由D是BC的中点可得BC=2CD=4![]() .在△ABC中,∠ACB=90°,由勾股定理得AB=
.在△ABC中,∠ACB=90°,由勾股定理得AB=![]() .再求得EB=EC=4,即可得四边形ACEB的周长.
.再求得EB=EC=4,即可得四边形ACEB的周长.
试题解析:解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD=![]() .
.
∵D是BC的中点,
∴BC=2CD=4![]() .
.
在△ABC中,∠ACB=90°,由勾股定理得AB=![]() .
.
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2![]() .
.


科目:初中数学 来源: 题型:
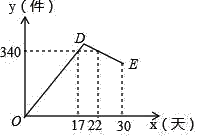
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期30天的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元.
(2)求线段DE所对应的函数关系式.(不要求写出自变量的取值范围)
(3)通过计算说明试销售期间第几天的日销售量最大?最大日销售量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
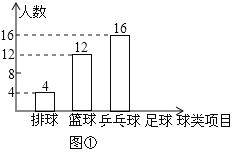

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,顺次连接
的中点,顺次连接![]() 所得的四边形我们称之为中点四边形,如图.
所得的四边形我们称之为中点四边形,如图.
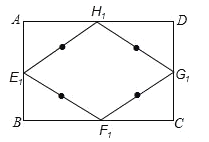
(1)求证:四边形![]() 是菱形;
是菱形;
(2)设![]() 的中点四边形是
的中点四边形是![]() ,
,![]() 的中点四边形是
的中点四边形是![]() ….
….![]() 的中点四边形是
的中点四边形是![]() ,那么这些中点四边形形状的变化有没有规律性? (填“有”或“无”)若有,说出其中的规律性 ;
,那么这些中点四边形形状的变化有没有规律性? (填“有”或“无”)若有,说出其中的规律性 ;
(3)进一步:如果我们规定:矩形![]() ,菱形
,菱形![]() ,并将矩形
,并将矩形![]() 的中点四边形用
的中点四边形用![]() 表示;菱形的中点四边形用
表示;菱形的中点四边形用![]() 表示,由题(1)知,
表示,由题(1)知,![]() ,那么
,那么![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O顺时针方向旋转90°,则图中阴影部分的面积是( )
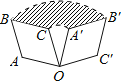
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
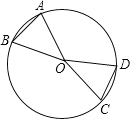
【题目】如图,OA,OB,OC,OD是⊙O的半径,
(1)如果∠AOB=∠COD,那么_______,_____=______,∠AOC______∠BOD;
(2)如果AB=CD,那么_____=_____,______;
(3)如果![]() =
=![]() ,那么____,_____,
,那么____,_____,![]() ______
______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景材料:
在学习全等三角形知识时,数学兴趣小组发现这样一个模型,它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们知道这种模型称为手拉手模型.
例如:如图1,两个等腰直角三角形△ABC和△ADE,∠BAC=∠EAD=90°,AB=AC,AE=AD,如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是手拉手模型,在这个模型中易得到△ABD≌△ACE.
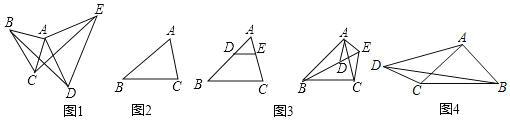
学习小组继续探究:
(1)如图2,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,请作出一个手拉手图形(尺规作图,不写作法,保留作图痕迹),并连接BE,CD,证明BE=CD;
(2)小刚同学发现,不等腰的三角形也可得到手拉手模型,例如,在△ABC中AB>AC,DE∥BC,将三角形ADE旋转一定的角度(如图3),连接CE和BD,证明△ABD∽△ACE.
学以致用:
(3)如图4,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα=![]() ,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com