
【题目】背景材料:
在学习全等三角形知识时,数学兴趣小组发现这样一个模型,它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们知道这种模型称为手拉手模型.
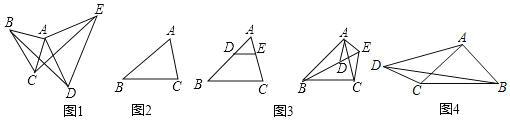
例如:如图1,两个等腰直角三角形△ABC和△ADE,∠BAC=∠EAD=90°,AB=AC,AE=AD,如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是手拉手模型,在这个模型中易得到△ABD≌△ACE.
学习小组继续探究:
(1)如图2,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,请作出一个手拉手图形(尺规作图,不写作法,保留作图痕迹),并连接BE,CD,证明BE=CD;
(2)小刚同学发现,不等腰的三角形也可得到手拉手模型,例如,在△ABC中AB>AC,DE∥BC,将三角形ADE旋转一定的角度(如图3),连接CE和BD,证明△ABD∽△ACE.
学以致用:
(3)如图4,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα=![]() ,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
【答案】(1)作图见解析,证明见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由等边三角形的性质可得AD=AB,AC=AE,∠DAB=∠EAC=60°,可得∠DAC=∠BAE,即可证△DAC≌△BAE,可得BD=CE;
(2)通过证明△ADE∽△ABC,可得![]() ,由旋转的性质可得∠BAC=∠DAE,即可得结论;
,由旋转的性质可得∠BAC=∠DAE,即可得结论;
(3)过点A 作AE垂直于AD,作∠AED=α,连接CE,则∠EDC=90°,通过证明△AEC∽△ADB,可得![]() ,由锐角三角函数和勾股定理可求AE,DE,EC的长,即可求BD的长.
,由锐角三角函数和勾股定理可求AE,DE,EC的长,即可求BD的长.
(1)作图
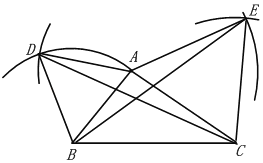
∵△ABD和△ACE都是等边三角形
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,且AD=AB,AC=AE
∴△DAC≌△BAE(SAS)
∴BE=CD
(2)如图,
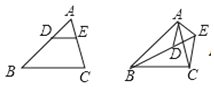
在第一个图中,∵DE∥BC
∴△ADE∽△ABC
∴![]()
∵将三角形ADE旋转一定的角度
∴∠BAC=∠DAE
∴∠BAD=∠CAE,且![]()
∴△ABD∽△ACE;
(3)如图,过点A 作AE垂直于AD,作∠AED=α,连接CE,则∠EDC=90°,
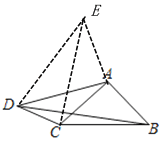
∵∠AED=∠ACB=α,∠CAB=∠DAE=90°
∴△AED∽△ACB
∴![]()
∵∠CAB=∠DAE=90°
∴∠CAE=∠DAB,且![]()
∴△AEC∽△ADB
∴![]()
∵△AED∽△ACB
∴∠ADE=∠ABC
∵∠ACB+∠ABC=90°,∠ADC=∠ACB
∴∠ADC+∠ADE=90°
∴∠EDC=90°
∵tanα=![]() ,AD=12.
,AD=12.
∴AE=16
∴DE=![]() =20
=20
∴EC=![]()
∵![]()
∴BD=![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
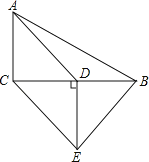
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为60元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b,且x=70时,y=50;x=80时,y=40;
(1)求出一次函数y=kx+b的解析式
(2)若该商场获得利润为w元,试写出利润w与销售单价x之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校九年级体育中考测试已结束,从中随机描取了50名男生的1000米测试成绩,根据评分标准按A、B、C、D四个等级进行统计,并然制成下面的扇形图和统计表
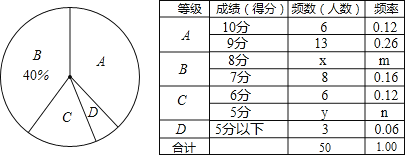
请你根据以上图表提供的信息,解答下列问题:
(1)在统计表中x= ,n= ;
(2)在扇形图中,A等级所对应的圆心角是 度;
(3)在50名学生的1000米跑成绩(得分)中,中位数是 ,众数是 ;
(4)如果我校九年级男生共有700名,那么请你估计这700名男生中成绩等级没有达到A或B的共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
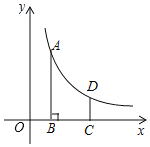
【题目】如图,反比例函数y=![]() (x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=
(x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=![]() .
.
(1)求反比例函数的表达式;
(2)若点P是y轴上一动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
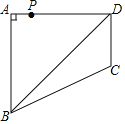
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,点P在四边形ABCD的边上,若点P到BD的距离为
,点P在四边形ABCD的边上,若点P到BD的距离为![]() ,则点P的个数为____个.
,则点P的个数为____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
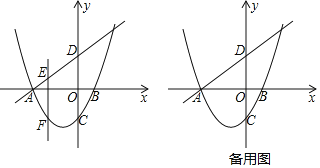
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com