
【题目】我校九年级体育中考测试已结束,从中随机描取了50名男生的1000米测试成绩,根据评分标准按A、B、C、D四个等级进行统计,并然制成下面的扇形图和统计表
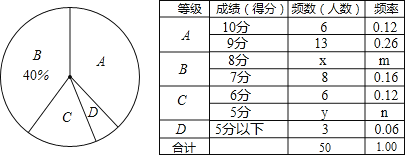
请你根据以上图表提供的信息,解答下列问题:
(1)在统计表中x= ,n= ;
(2)在扇形图中,A等级所对应的圆心角是 度;
(3)在50名学生的1000米跑成绩(得分)中,中位数是 ,众数是 ;
(4)如果我校九年级男生共有700名,那么请你估计这700名男生中成绩等级没有达到A或B的共有 人.
【答案】(1) 12,0.04;(2)136.8;(3)8 分,9 分;(4)154.
【解析】
( 1 )x=50×40%﹣8=12,m=12÷50=0.24,n=1﹣0.12﹣0.26﹣﹣0.24﹣0.16﹣0.12﹣0.06=0.04;
( 2 )A等级所对应的圆心角360°×(0.12+0.26)=136.8°,
( 3 )中位数为第25、26个同学的平均数:8分,9分的人数最多,共13人次,所以众数为9分;
( 4 )700名男生中成绩等级没有达到A或B的共有700×(0.12+0.04+0.06)=154(人).
( 1 )x=50×40%﹣8=12,
m=12÷50=0.24,n=1﹣0.12﹣0.26﹣﹣0.24﹣0.16﹣0.12﹣0.06=0.04,
故答案为12,0.04;
( 2 )A等级所对应的圆心角360°×(0.12+0.26)=136.8°,
故答案为 136.8;
( 3 )中位数为第25、26个同学的平均数:8分,
9分的人数最多,共13人次,所以众数为9分,
故答案为,9 分;
( 4 )700名男生中成绩等级没有达到A或B的共有700×(0.12+0.04+0.06)=154(人)
故答案为154.


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
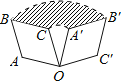
【题目】如图菱形OABC中,∠A=120°,OA=1,将菱形OABC绕点O顺时针方向旋转90°,则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.若该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前七个月的利润总和与t之间的关系)为s=![]() t2-2t.
t2-2t.
(1)第几个月末时,公司亏损最多?为什么?
(2)第几个月末时,公司累积利润可达30万元?
(3)求第8个月公司所获利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景材料:
在学习全等三角形知识时,数学兴趣小组发现这样一个模型,它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们知道这种模型称为手拉手模型.
例如:如图1,两个等腰直角三角形△ABC和△ADE,∠BAC=∠EAD=90°,AB=AC,AE=AD,如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是手拉手模型,在这个模型中易得到△ABD≌△ACE.
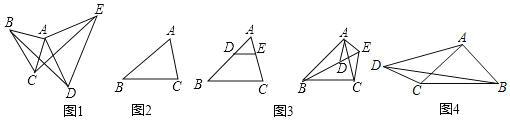
学习小组继续探究:
(1)如图2,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,请作出一个手拉手图形(尺规作图,不写作法,保留作图痕迹),并连接BE,CD,证明BE=CD;
(2)小刚同学发现,不等腰的三角形也可得到手拉手模型,例如,在△ABC中AB>AC,DE∥BC,将三角形ADE旋转一定的角度(如图3),连接CE和BD,证明△ABD∽△ACE.
学以致用:
(3)如图4,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα=![]() ,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
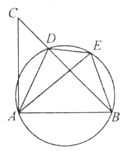
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校践行素质教育,提供了“乒乓球”,“舞蹈”,“写作”和“航模”四种校本课程供学生选择(每位学生必须且只能选择其中一门)。学生会在全校范围内随机抽取了部分学生进行调查,并将调查结果给制成如图所示的统计图(均不完整).
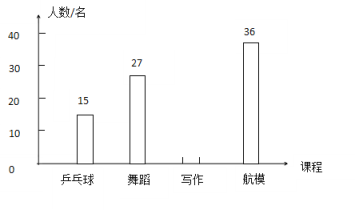
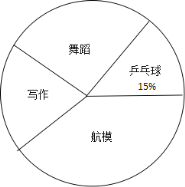
请你根据统计图提供的信息解决下列问题.
(1)本次调查的学生总人数是 名,在统计图中,补全条形图;
(2)请估计该校1500名学生中选择“写作”课程的人数;
(3)学校将选择“航模”课程的学生分成人数相等的A,B,C三个班,宁宁和静静都选择了“航模”课程.已知宁宁不在A班,求她们被分到同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
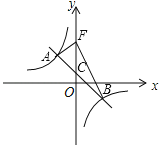
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com