
【题目】如图,△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数.
(2)若△APQ周长为12,BC长为8,求PQ的长.

【答案】(1)∠PAQ=20°;(2)PQ=2.
【解析】
(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,根据线段垂直平分线的性质得:AP=PB,AQ=CQ,由等腰三角形的性质得:∠B=∠BAP=x+z,∠C=∠CAQ=x+y,再由三角形内角和定理相加可得结论;
(2)根据△APQ周长为12,列等式为AQ+PQ+AP=12,由等量代换得BC+2PQ=12,可得PQ的长.
(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ,
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y,
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°,
∴x=20°,
∴∠PAQ=20°;
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12,
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,
即CQ+BQ+2PQ=12,
BC+2PQ=12,
∵BC=8,
∴PQ=2.


科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
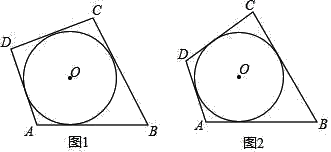
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的4月23日被联合国教科文组织确定为“世界读书日”.为满足同学们的读书需某校图书室在今年“世界读书日”期间准备到书店购买文学名著和科普读物两类图书.已知20本文学名著和40本科普读物共需1520元,20本文学名著比20本科普读物多440元(注:所采购的文学名著价格都一样,所购买的科普读物的价格都一样).
(1)每本文学名著和科普读物各多少元?
(2)若学校要求购买科普读物比文学名著多20本,科普读物和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
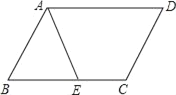
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E.
(1)在AD上求作点F,使点F到CD和BC的距离相等;
(要求:尺规作图,保留作图痕迹,不写作法)
(2)判断四边形AECF是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
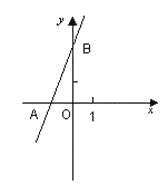
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
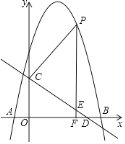
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com