
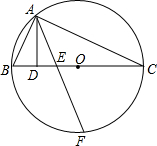
 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是 |
| BC |
| 2 |
| AB |
| BE |
| AC |
| CE |
| AB |
| BE |
| BF |
| EF |
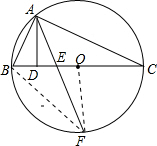 解:
解: |
| BC |
| 2 |
| AB |
| BE |
| AC |
| CE |
| BE |
| CE |
| 6 |
| 8 |
| 3 |
| 4 |
| 30 |
| 7 |
| AB |
| BE |
| BF |
| EF |
| 6 | ||
|
5
| ||
| EF |
25
| ||
| 7 |
25
| ||
| 7 |


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?
在400米的环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两地同时出发,按逆时针方向跑步,甲每秒5米,乙每秒4米,每人跑100米都要停留10秒钟,那么甲追上乙需要多少秒?查看答案和解析>>
科目:初中数学 来源: 题型:
 若有理数a、b,它们在数轴上的对应点的位置如图,把a、b、-a、-b按照从小到大的顺序排列,正确的是( )
若有理数a、b,它们在数轴上的对应点的位置如图,把a、b、-a、-b按照从小到大的顺序排列,正确的是( )| A、-b<a<-a<b |
| B、a<-b<-a<b |
| C、-b<-a<a<b |
| D、a<-a<-b<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com