
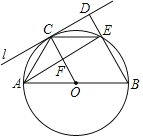
【题目】如图,AB为⊙O的直径,C为半圆上一动点,过点C作⊙O的切线l,过点B作BD⊥l,垂足为D,BD与⊙O交于点E,连接OC,CE,AE,AE交OC于点F.
(1)求证:△CDE≌△EFC;
(2)若AB=4,连接AC.
①当AC=_____时,四边形OBEC为菱形;
②当AC=_____时,四边形EDCF为正方形.
【答案】(1)详见解析;(2)①当AC=2时,四边形OCEB是菱形时2;②当四边形DEFC是正方形时,2![]() .
.
【解析】
(1)由AB是直径可得∠AEB=90°,由切线性质可得∠FCD=90°,由BD⊥CD可得∠CDE=90°,即可证明四边形CFED是矩形,可得CF=DE,EF=CD,利用SSS即可证明△CDE≌△EFC;(2)①连接OE,由菱形性质可得OB=BE,即可证明△OBE是等边三角形,可得∠B=60°,由OC//BD可得∠AOC=∠B=60°,可证明△OAC是等边三角形,即可求出AC=![]() AB=2;②由正方形的性质可得∠CEF=∠FCE=45°,由垂径定理可知
AB=2;②由正方形的性质可得∠CEF=∠FCE=45°,由垂径定理可知![]() ,即可得出AC=CE,进而可得∠CAE=∠CEA=45°,即可证明∠ACE=90°,可得AE是⊙O的直径,即点E与点B重合,点F与点O重合,可得△ABC是等腰直角三角形,即可求出AC的长.
,即可得出AC=CE,进而可得∠CAE=∠CEA=45°,即可证明∠ACE=90°,可得AE是⊙O的直径,即点E与点B重合,点F与点O重合,可得△ABC是等腰直角三角形,即可求出AC的长.
(1)∵BD⊥CD,
∴∠CDE=90°,
∵AB是直径,
∴∠AEB=90°,
∵CD是切线,
∴∠FCD=90°,
∴四边形CFED矩形,
∴CF=DE,EF=CD,
在△CDE和△EFC中,
 ,
,
∴△CDE≌△EFC.
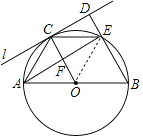
(2)解:①当AC=2时,四边形OBEC是菱形.
理由:连接OE.
∵四边形OBEC是菱形,
∴OB=BE,
∵OE=OB,
∴△OBE是等边三角形,
∴∠B=60°,
∵OC//BD,
∴∠AOC=∠B=60°,
∵OA=OC,
∴△OAC是等边三角形,
∴AC=OA=![]() AB=2.
AB=2.
∴AC=2时,四边形OBEC是菱形.
故答案为2.
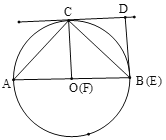
②当四边形EDCF是正方形时,
∵CF=FE,
∵∠CEF=∠FCE=45°,
∵OC⊥AE,
∴![]() ,
,
∴AC=CE,
∴∠CAE=∠CEA=45°,
∴∠ACE=90°,
∴AE是⊙O的直径,即点E与点B重合,点F与点O重合,
∴△ABC是等腰直角三角形,
∴AC=![]() AB=2
AB=2![]() .
.
∴AC=2![]() 时,四边形EDCF是正方形.
时,四边形EDCF是正方形.
故答案为2![]() .
.


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=4,点E,F分别为BC,AC上的两个动点,将△CEF沿EF折叠,点C的对应点为G,若点G落在射线AB上,且△AGF恰为直角三角形,则线段CF的长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
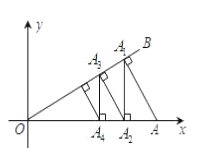
【题目】.如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(4,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2019坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的菱形OABC中,∠AOC=60°,以顶点O为圆心、对角线OB的长为半径作弧,与射线OA,OC分别交于点D,E,则图中阴影部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
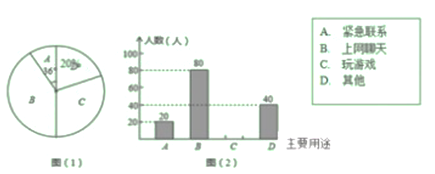
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,随机抽查了某中学九年级的同学,关于手机在中学生中的主要用途做了调查,对调查数据进行统计整理、制作了如下的两种统计图:请根据图形回答问题
(1)这次被调查的学生共有______人,其中主要用于“上网聊天”的学生人数占抽样人数的百分比为_____;
(2)请你将条形统计图(2)补充完整;
(3)若该校共有3000名学生,请你估计主要使用手机玩游戏的人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 km/h;
(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com