
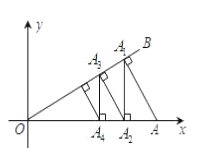
【题目】.如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(4,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2019坐标为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
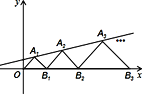
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
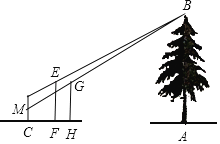
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
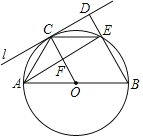
【题目】如图,AB为⊙O的直径,C为半圆上一动点,过点C作⊙O的切线l,过点B作BD⊥l,垂足为D,BD与⊙O交于点E,连接OC,CE,AE,AE交OC于点F.
(1)求证:△CDE≌△EFC;
(2)若AB=4,连接AC.
①当AC=_____时,四边形OBEC为菱形;
②当AC=_____时,四边形EDCF为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
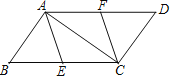
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com