
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,

(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,AC=17,求CF的长.
(1)证明见解析;(2)8.
【解析】
试题分析:(1)首先利用角平分线的性质得出CF=CE,进而利用HL定理得出Rt△CFD≌Rt△CEB;
(2)首先得出Rt△CFA≌Rt△CEA,进而得出AF=AE,设DF=x,则9+x=21-x,求出x即可得出AE的长,然后利用勾股定理即可求出CF的长..
试题解析:(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△CFD和Rt△CEB中,
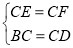 ,
,
∴Rt△CFD≌Rt△CEB(HL);
(2)【解析】
∵在Rt△CFA和Rt△CEA中,
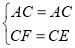 ,
,
∴Rt△CFA≌Rt△CEA(HL),
∴AF=AE,设DF=x,
则9+x=21-x,
解得:x=6,
故AE=21-6=15.
在Rt△ACF中,CF=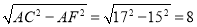 .
.
考点:全等三角形的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片七年级上学期期中考试数学试卷(解析版) 题型:填空题
若 、
、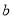 互为相反数,
互为相反数, 、
、 互为倒数,
互为倒数,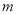 到原点的距离为2,则代数式|m|-cd+
到原点的距离为2,则代数式|m|-cd+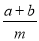 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.

(1)填空:双曲线的另一支在第 象限, 的取值范围是 ;
的取值范围是 ;
(2)若点C的坐标为(1,1),请用含有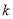 的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若 ,
, ,求双曲线的解析式.
,求双曲线的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图在等腰Rt△ABC中,∠C=90o,AC=3,D是AC上一点,若tan∠DBA= ,则AD的长为 ( )
,则AD的长为 ( )

A.2 B.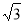 C.
C. D.1
D.1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图所示, AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市七年级上学期期中考试数学试卷(解析版) 题型:选择题
有理数a、b在数轴上的位置如图所示,则化简 的结果为( )
的结果为( )

A.2a B.-2b C.-2a D.2b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com