
(本题10分)如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.

(1)填空:双曲线的另一支在第 象限, 的取值范围是 ;
的取值范围是 ;
(2)若点C的坐标为(1,1),请用含有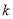 的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若 ,
, ,求双曲线的解析式.
,求双曲线的解析式.
(1)三,k>0;(2)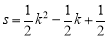 ,E点的坐标为(1,
,E点的坐标为(1,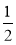 ),即E点为BC的中点,阴影部分的面积S最小;(3)
),即E点为BC的中点,阴影部分的面积S最小;(3)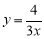 .
.
【解析】
试题分析:(1)根据反比例函数图象与性质得到:双曲线 的一支在第一象限,则k>0,得到另一支在第三象限;
的一支在第一象限,则k>0,得到另一支在第三象限;
(2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(1,1),则A点的纵坐标为1,E点的横坐标为1,B点坐标为(1,0),再分别把y=1或x=1代入 可得到A点的坐标为(k,1),E点的坐标为(1,k),然后计算S阴影部分=S△ACE+S△OBE=
可得到A点的坐标为(k,1),E点的坐标为(1,k),然后计算S阴影部分=S△ACE+S△OBE=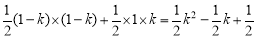 ,配方得
,配方得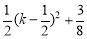 ,当k=
,当k=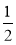 时,S阴影部分最小值为
时,S阴影部分最小值为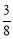 ,则E点的坐标为(1,
,则E点的坐标为(1,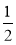 ),即E点为BC的中点;
),即E点为BC的中点;
(3)设D点坐标为(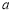 ,
,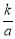 ),由
),由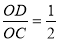 ,则2OD=OC,即D点为OC的中点,于是C点坐标为(
,则2OD=OC,即D点为OC的中点,于是C点坐标为(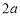 ,
,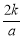 ),得到A点的纵坐标为
),得到A点的纵坐标为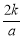 ,把
,把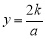 代入
代入 得
得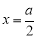 ,确定A点坐标为(
,确定A点坐标为(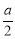 ,
,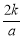 ),根据三角形面积公式由S△OAC=2得到
),根据三角形面积公式由S△OAC=2得到 ,然后解方程即可求出k的值.
,然后解方程即可求出k的值.
试题解析:(1)三,k>0;
(2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,而点C的坐标为(1,1),
∴A点的纵坐标为1,E点的横坐标为1,B点坐标为(1,0),
把y=1代入 得x=k;把x=1代入
得x=k;把x=1代入 得y=k,
得y=k,
∴A点的坐标为(k,1),E点的坐标为(1,k),
∴S阴影部分=S△ACE+S△OBE=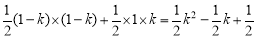 =
=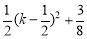 ,
,
当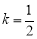 时,S阴影部分最小,最小值为
时,S阴影部分最小,最小值为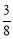 ;
;
∴E点的坐标为(1,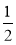 ),即E点为BC的中点,
),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)设D点坐标为(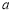 ,
,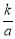 ),∵
),∵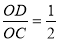 ,∴2OD=OC,即D点为OC的中点,
,∴2OD=OC,即D点为OC的中点,
∴C点坐标为(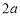 ,
,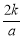 ),∴A点的纵坐标为
),∴A点的纵坐标为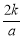 ,
,
把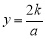 代入
代入 得
得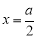 ,∴A点坐标为(
,∴A点坐标为(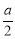 ,
,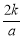 ),
),
∵S△OAC=2,∴ ,∴
,∴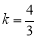 ,∴双曲线的解析式为
,∴双曲线的解析式为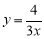 .
.
考点:反比例函数综合题.


科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片九年级上学期期中考试数学试卷(解析版) 题型:填空题
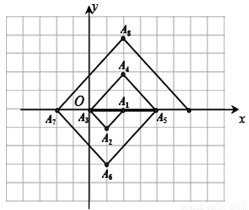
如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2017的坐标为 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片七年级上学期期中考试数学试卷(解析版) 题型:选择题
下面的计算正确的是( )
A. 6a-5a=1 B. a+2a2=3a3 C.-(a-b)=-a+b D.2(a+b)=2a+b
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE等于( )

A.40° B.45° C.55° D.35°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:填空题
一个三角形的两边长分别为4cm和7cm,第三边长是一元二次方程 的实数根,则三角形的周长是 cm.
的实数根,则三角形的周长是 cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,

(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,AC=17,求CF的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,反比例函数y= (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com