
科目:初中数学 来源: 题型:解答题
| 每户居民一个月用水量的范围 | 水费价格(范围:元/立方米) |
| 不超过20立方米 | a |
| 超过20立方米 | 不超过部分仍为a元,超过部分为b元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
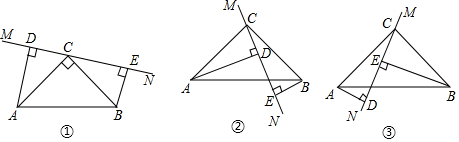
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
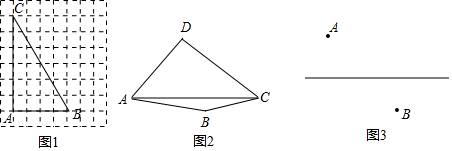
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
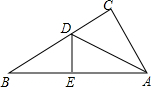 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直径AD折叠,使点C恰好与AB边上的点E重合,求出CD的长.
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直径AD折叠,使点C恰好与AB边上的点E重合,求出CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
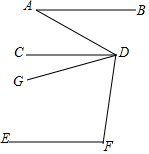 如图,已知AB∥CD∥EF,且∠A=50°,∠F=120°,DG平分∠ADF,求∠CDG的度数.
如图,已知AB∥CD∥EF,且∠A=50°,∠F=120°,DG平分∠ADF,求∠CDG的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com