
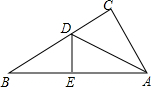
 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直径AD折叠,使点C恰好与AB边上的点E重合,求出CD的长.
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直径AD折叠,使点C恰好与AB边上的点E重合,求出CD的长. 分析 首先利用勾股定理求出AB,设CD=DE=x,在Rt△BDE中,根据BD2=BE2+DE2,列出方程即可解决问题.
解答 解:∵AC=AC=6,CD=ED,∠C=∠AED=90°,
在Rt△ABC中,AC=6,BC=8,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴BE=AB-AE=4,设CD=DE=x,
在Rt△BDE中,∵BD2=BE2+DE2,
∴(8-x)2=42+x2,
∴x=3,
∴CD=3.
点评 本题考查翻折变换、勾股定理等知识,解题的关键是灵活运用勾股定理,学会利用参数,构建方程解决问题,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=3,BC=4,CA=8 | B. | ∠A=60°,∠B=45°,AB=4 | ||
| C. | AB=4,BC=3,∠A=30° | D. | ∠C=90°,AB=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,已知AB=2,BC=1.5,矩形在直线上绕其右下角的顶点B向右第一次旋转90°至图①位置,再绕右下角的顶点继续向右第二次旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是1512π.
如图,在矩形ABCD中,已知AB=2,BC=1.5,矩形在直线上绕其右下角的顶点B向右第一次旋转90°至图①位置,再绕右下角的顶点继续向右第二次旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是1512π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com