
【题目】某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台.三种型号的空调进价和售价如下表:
种类价格 | 甲 | 乙 | 丙 |
进价(元/台) | 1600 | 1800 | 2400 |
售价(元/台) | 1800 | 2050 | 2600 |
商场计划投入总资金5万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半.若设购买甲型号空调x台,所有型号空调全部售出后获得的总利润为W元.
(1)求W与x之间的函数关系式.
(2)商场如何采购空调才能获得最大利润?
(3)由于原材料上涨,商场决定将丙型号空调的售价提高a元(a≥100),其余型号售价不变,则商场又该如何采购才能获得最大利润?
【答案】(1)![]() =
=![]() ,(2)购进甲10台,乙5台,丙10台时利润最大
,(2)购进甲10台,乙5台,丙10台时利润最大
(3)即购进甲12台,乙1台,丙12台.
【解析】解:(1)由题意知:丙型号为![]() 台,乙型号为
台,乙型号为![]() 台,则
台,则
![]()
=![]() ………………………………………………………………2分
………………………………………………………………2分
(2)依题意得: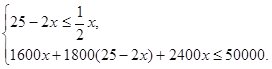 ……………………………3分
……………………………3分
解得![]() ………………………………………………………………4分
………………………………………………………………4分
又![]() 为正整数
为正整数
![]() 取10,11,12 ………………………………………………………………5分
取10,11,12 ………………………………………………………………5分
![]() 随
随![]() 增大而减小
增大而减小
![]() 当
当![]() 时,
时, ![]() 最大.
最大.
即购进甲10台,乙5台,丙10台时利润最大.……………………………………6分
(3)依题意得: ![]()
![]() ………………………………………………8分
………………………………………………8分
![]() 当
当![]() 时,
时, ![]() ,所以有三种方案:
,所以有三种方案:
即购进甲、丙两种型号各10台,乙5台
或购进甲、丙两种型号各11台,乙3台
或购进甲、丙两种型号各12台,乙1台
![]() 当
当![]() 时,
时, ![]() ,所以当
,所以当![]() 取12时,
取12时, ![]() 最大.
最大.
即购进甲12台,乙1台,丙12台.………………………………………10分
(1)总利润=甲型号空调利润+乙型号空调利润+丙型号空调利润,根据此关系计算即可;
(2)据题意列表达式组求解;
用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解
(3)根据(1)中的等量关系可得出一个关于总利润和a的函数关系式,根据函数性质和a的取值范围,判断出不同情况下哪种利润最大.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC, DC⊥BC,AE平分∠BAD,下列结论: ① ∠A E D =90°;
② ∠A D E = ∠ C D E ; ③ D E = B E ;④ AD=AB+CD, 四个结论中成立的是( )
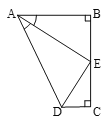
A. ① ② ④ B. ① ② ③ C. ② ③ ④ D. ② ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对七年级学生数学学期成绩的评价规定如下:学期评价得分由期末测试成绩(满分100分)和期中测试成绩(满分100分)两部分组成,其中期末测试成绩占70%,期中测试成绩占30%,当学期评价得分大于或等于85分时,该生数学学期成绩评价为优秀.
(1)小明的期末测试成绩和期中成绩两项得分之和为170分,学期评价得分为87分,则小明期末测试成绩和期中测试成绩各得多少分?
(2)某同学期末测试成绩为75分,他的综合评价得分有可能达到优秀吗?为什么?
(3)如果一个同学学期评价得分要达到优秀,他的期末测试成绩至少要多少分(结果保留整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
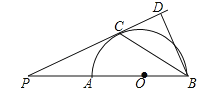
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com