
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
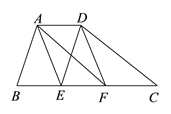
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
【答案】(1)![]() ,理由见解析;(2)见解析
,理由见解析;(2)见解析
【解析】
(1)由四边形AEFD是平行四边形可得AD=EF,根据条件可证四边形ABED是平行四边形, 四边形AFCD是平行四边形,所以AD=BE,AD=FC,所以AD=![]() BC;
BC;
(2)根据矩形的判定和定义,对角线相等的平行四边形是矩形.只要证明AF=DE即可得出结论.
证明:(1)AD=![]() BC
BC
理由如下:
∵AD∥BC,AB∥DE,AF∥DC,
∴四边形ABED和四边形AFCD都是平行四边形.
∴AD=BE,AD=FC,
又∵四边形AEFD是平行四边形,
∴AD=EF.
∴AD=BE=EF=FC.
∴![]() ;
;
(2)证明:∵四边形ABED和四边形AFCD都是平行四边形,
∴DE=AB,AF=DC.
∵AB=DC,
∴DE=AF.
又∵四边形AEFD是平行四边形,
∴平行四边形AEFD是矩形.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图像如图所示,则下列结论正确的个数有( )
①c>0;②b2-4ac<0;③ a-b+c>0;④当x>-1时,y随x的增大而减小.
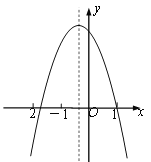
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为![]() ,
,![]() ,点M是AO中点,
,点M是AO中点,![]() 的半径为2.
的半径为2.
![]() 若
若![]() 是直角三角形,则点P的坐标为______
是直角三角形,则点P的坐标为______![]() 直接写出结果
直接写出结果![]()
![]() 若
若![]() ,则BP与
,则BP与![]() 有怎样的位置关系?为什么?
有怎样的位置关系?为什么?
![]() 若点E的坐标为
若点E的坐标为![]() ,那么
,那么![]() 上是否存在一点P,使
上是否存在一点P,使![]() 最小,如果存在,求出这个最小值,如果不存在,简要说明理由.
最小,如果存在,求出这个最小值,如果不存在,简要说明理由.
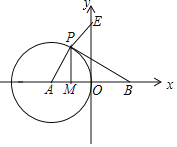
查看答案和解析>>
科目:初中数学 来源: 题型:
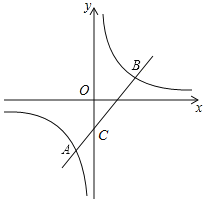
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数y=![]() (k2≠0)的图象交于A(-1,-4)和点B(4,m)
(k2≠0)的图象交于A(-1,-4)和点B(4,m)
(1)求这两个函数的解析式;
(2)已知直线AB交y轴于点C,点P(n,0)在x轴的负半轴上,若△BCP为等腰三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到C处有生命迹象.已知A,B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
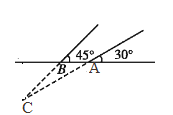
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念“五四运动”100周年,某校举行了征文比赛,该校学生全部参加了比赛.比赛设置一等、二等、三等三个奖项,赛后该校对学生获奖情况做了抽样调查,并将所得数据绘制成如图所示的两幅不完整的统计图.根据图中信息解答下列问题:
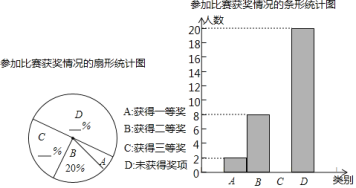
(1)本次抽样调查学生的人数为 .
(2)补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.
(3)若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
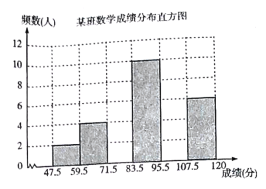
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x(x﹣b)﹣![]() 与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
(1)若点B与点C关于直线x=1对称,求b的值;
(2)若OB=OA,求△BCP的面积;
(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h,求出h与b的关系;若h有最大值或最小值,直接写出这个最大值或最小值.
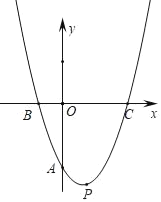
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com