
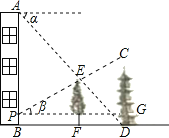
【题目】如图,在一居民楼AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为38°.从距离楼底B点2米的P处经过树顶E点恰好看到塔的顶部C点,且仰角β为28°.已知树高EF=8米,求塔CD的高度.(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,以AB为直径的O交BC于D,点E为AC的中点,连接DE.
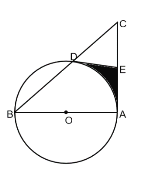
(1)求证:DE是O的切线;
(2)若∠BAD=50°,AC=6,CD=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
(1)求证:AC是⊙O的切线;
(2)若![]() ,BD=5,求BF的长.
,BD=5,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
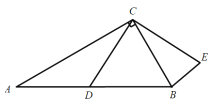
【题目】如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
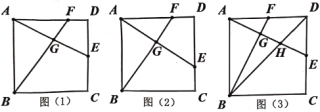
【题目】如图,正方形ABCD的边长为6,E、F分别是边CD、AD上动点,AE和BF交于点G.
(1)如图(1),若E为边CD的中点,AF=2FD,求AG的长.
(2)如图(2),若点F在AD上从A向D运动,点E在DC上从D向C运动,两点同时出发,同时到达各自终点,求在运动过程中,点G运动的路径长.
(3)如图(3),若E、F分别是边CD、AD上的中点,BD与AE交于点H,求∠FBD的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
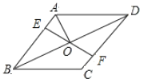
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
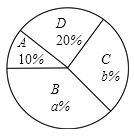
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,已知线段![]() ,现要在该网格内再确定格点
,现要在该网格内再确定格点![]() 和格点
和格点![]() ,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )
,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )

A.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为正方形的有2种;
为正方形的有2种;
B.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为菱形的(正方形除外)有3种;
为菱形的(正方形除外)有3种;
C.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为矩形的(正方形除外)有两种;
为矩形的(正方形除外)有两种;
D.不存在以![]() 为对角线的四边形
为对角线的四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com