
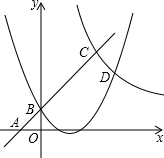
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+1�ֱ�x��y���ڵ�A��B����˫����$y=\frac{k}{x}��k��0��$�ڵ�C��3��n����������$y=\frac{1}{2}{x^2}+bx+c$����B�������˫���߽��ڵ�D����D��������Ϊ3��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+1�ֱ�x��y���ڵ�A��B����˫����$y=\frac{k}{x}��k��0��$�ڵ�C��3��n����������$y=\frac{1}{2}{x^2}+bx+c$����B�������˫���߽��ڵ�D����D��������Ϊ3������ ��1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�B��C��D�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2�����ݺ���ֵ���ɵ���Ӧ�Ա�����ֵ�����ݺ���ֵ��ȵ������ľ����ǽϴ�ĺ�����С�ľ���ֵ���ɵô𰸣�
��3�������Ա�����ȵ������ľ����ǽϴ�����������С�������꣬�ɵú�����ϵʽ�����ݶ��κ��������ʣ��ɵô𰸣�
��� �⣺��1����x=3ʱ��y=x+1=4����C��3��4������x=0ʱ��y=x+1=1����B��0��1����
��C�㣨3��4������˫���ߣ���
4=$\frac{k}{3}$�����k=12��
˫���ߵĽ���ʽΪy=$\frac{12}{x}$��
��y=3ʱ��3=$\frac{12}{x}$�����x=4����D��4��3����
��B��D��������������ߣ���
$\left\{\begin{array}{l}{\frac{1}{2}��{4}^{2}+4b+c=3}\\{c=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=1}\end{array}\right.$��
�����ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x+1��
��2����y=2ʱ��$\frac{1}{2}$x2-$\frac{3}{2}$x+1=2�����x1=$\frac{3+\sqrt{17}}{2}$��x2=$\frac{3-\sqrt{17}}{2}$��
��F1��$\frac{3+\sqrt{17}}{2}$��2����F2��$\frac{3-\sqrt{17}}{2}$��2����
��y=2ʱ��2=$\frac{12}{x}$�����x=6����E��6��0����
EF1=6-$\frac{3+\sqrt{17}}{2}$=$\frac{9-\sqrt{17}}{2}$��
EF2=6-$\frac{3-\sqrt{17}}{2}$=$\frac{9+\sqrt{17}}{2}$��
��3����-1��m��0ʱ��d=$\frac{1}{2}$m2-$\frac{3}{2}$m+1-��m+1��=$\frac{1}{2}$m2-$\frac{5}{2}$m=$\frac{1}{2}$��m-$\frac{5}{2}$��2-$\frac{25}{8}$
��0��m��3ʱ��d=m+1-��$\frac{1}{2}$m2-$\frac{3}{2}$m+1��=-$\frac{1}{2}$m2+$\frac{5}{2}$m=-$\frac{1}{2}$��m-$\frac{5}{2}$��2+$\frac{25}{8}$����m=$\frac{5}{2}$ʱ��d���=$\frac{25}{8}$��
��3��m��4ʱ��d=$\frac{12}{m}$-��$\frac{1}{2}$m2-$\frac{3}{2}$m+1����
d��m���������Сʱm��ȡֵ��Χ��-1��m��0��$\frac{5}{2}$��m��4��
���� ���⿼���˶��κ������ۺ��⣬�����˴���ϵ������������ʽ������ֵ��ȵ������ľ����ǽϴ�ĺ�����С�ľ���ֵ���Ա�����ȵ������ľ����ǽϴ�����������С�������꣬�������˶��κ��������ʣ�a��0ʱ���Գ������࣬y��x���������С��a��0ʱ���Գ�����Ҳ࣬y��x���������С��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
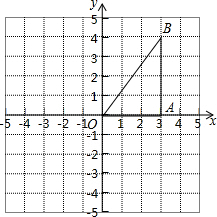 ��10��10������ֽ�Ͻ���ƽ��ֱ������ϵ��ͼ��ʾ����ֱ��������ABO�У���OAB=90�㣬�ҵ�B������Ϊ��3��4����
��10��10������ֽ�Ͻ���ƽ��ֱ������ϵ��ͼ��ʾ����ֱ��������ABO�У���OAB=90�㣬�ҵ�B������Ϊ��3��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
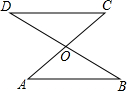 ��ͼ��AC��BD���ڵ�O��ͼ�й���8���߶Σ����Ƿֱ���CD��OC��OA��OD��OB��BD��AC��AB��
��ͼ��AC��BD���ڵ�O��ͼ�й���8���߶Σ����Ƿֱ���CD��OC��OA��OD��OB��BD��AC��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4x=2x-1����4x-2x=1 | B�� | ��-2x=4����x=2 | ||
| C�� | ��5x-3=4����5x=4-3 | D�� | ��-3x-2=2x+3����-3x-2x=3+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
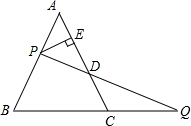 ��ͼ��P�ǵȱߡ�ABC��AB����һ�㣬��P��PE��AC��E����BC���ӳ����Ͻ�ȡCQ=AP������PQ��AC�ڵ�D��
��ͼ��P�ǵȱߡ�ABC��AB����һ�㣬��P��PE��AC��E����BC���ӳ����Ͻ�ȡCQ=AP������PQ��AC�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com