
【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示. 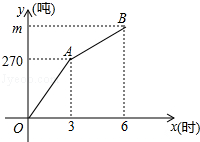
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式.
【答案】
(1)270
(2)解:乙队调离前,甲、乙两队每小时的清雪总量为 ![]() =90吨;
=90吨;
∵乙队每小时清雪50吨,
∴甲队每小时的清雪量为:90﹣50=40吨,
∴m=270+40×3=390吨,
∴此次任务的清雪总量为390吨
(3)解:由(2)可知点B的坐标为(6,390),设乙队调离后y与x之间的函数关系式为:y=kx+b(k≠0),
∵图象经过点A(3,270),B(6,390),
∴ ![]()
解得 ![]()
∴乙队调离后y与x之间的函数关系式:y=40x+150
【解析】解:(1)由函数图象可以看出乙队调离时,甲、乙两队已完成的清雪总量为270吨; 故答案为:270.
(1)由函数图象可以看出乙队调离时,甲、乙两队已完成的清雪总量为 270吨;(2)先求出甲队每小时的清雪量,再求出m.(3)设乙队调离后y与x之间的函数关系式为:y=kx+b,把A,B两点代入求出函数关系式.


科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在 ![]() 上找一点P,使得
上找一点P,使得 ![]() =
= ![]() ,以下是甲、乙两人的作法: 甲:⑴取AB中点D
,以下是甲、乙两人的作法: 甲:⑴取AB中点D
⑵过D作直线AC的平行线,交 ![]() 于P,则P即为所求
于P,则P即为所求
乙:⑴取AC中点E
⑵过E作直线AB的平行线,交 ![]() 于P,则P即为所求
于P,则P即为所求
对于甲、乙两人的作法,下列判断何者正确?( )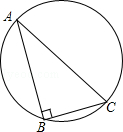
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误C
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式的排列规律:3x,![]() ,照这样排列第10个单项式应是
,照这样排列第10个单项式应是![]()
![]()
A. 39x10 B. -39 x10 C. -43 x10 D. 43 x10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为 ![]() 的中点,连接DE,EB.
的中点,连接DE,EB. 
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射,若被
反射,若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且
平行,且![]() ,则
,则![]() _________,
_________,![]() ________.
________.
(2)在(1)中,若![]() ,则
,则![]() _______;若
_______;若![]() ,则
,则![]() ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜![]() 、
、![]() 的夹角
的夹角![]() ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请说明理由.
平行.请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合并下列多项式中的同类项:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣![]() a2b
a2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com