
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为 ![]() 的中点,连接DE,EB.
的中点,连接DE,EB. 
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
【答案】
(1)证明:∵CD是⊙O的切线,∴∠CDO=90°,∵∠BOD=60°,
∴∠C=30°,∠AOD=120°,
∵E为 ![]() 的中点,
的中点,
∴∠AOE=∠DOE=60°,
∴∠BOE=120°,
∵OE=OB,
∴∠OEB=∠OBE=30°,
∴∠C=∠OBE=∠E,
∴DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形
(2)解:连接OE,由(1)知, ![]() ,
,
∴∠BOE=120°,
∵阴影部分面积为6π,
∴ ![]() =6π,
=6π,
∴r=6.

【解析】(1)由∠BOD=60°E为 ![]() 的中点,得到
的中点,得到 ![]() ,于是得到DE∥BC,根据CD是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得四边形BCDE是平行四边形;(2)连接OE,由(1)知,
,于是得到DE∥BC,根据CD是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得四边形BCDE是平行四边形;(2)连接OE,由(1)知, ![]() ,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.
,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)小宁和婷婷在一起做拼图游戏,他们用 “![]() 、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:
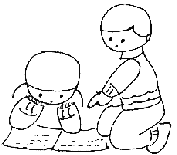
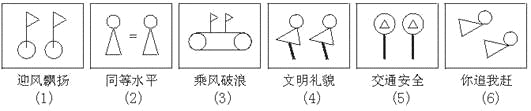
观察以上图案
(1)这个图案有什么特点?
(2)它可以通过一个“基本图案”经过怎样的平移而形成?
(3)在平移的过程中,“基本图案”的大小、形状、位置是否发生了变化?你能解释其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,3,0,4;
(2)用“<”号将(1)中各数连接起来;
(3)直接填空:数轴上表示3和表示1的两点之间的距离是_____,数轴上A点表示的数为4,B点表示的数为﹣2,则A、B之间的距离是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示. 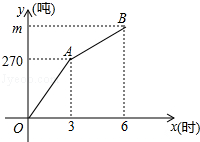
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 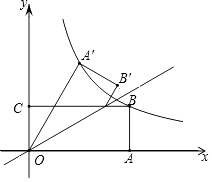
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com