
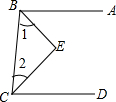
 已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.
已知,如图,BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,求证:AB∥CD.分析 先根据角平分线的定义得出∠ABC=2∠1,∠BCD=2∠2,再由∠1+∠2=90°可得出∠ABC+∠BCD=180°,由此可得出结论.
解答 证明:∵BE平分∠ABD(已知),
∴∠ABC=2∠1(角平分线的定义).
∵CE平分∠DCB(已知),
∴∠BCD=2∠2(角平分线的定义),
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)(等式的性质)
又∵∠1+∠2=90°(已知)
∴∠ABC+∠BCD=2×90°=180°,
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:已知;∠ABC=2∠1;角平分线的定义;∠BCD=2∠2;等式的性质;∠1+∠2=90°;已知;∠ABC+∠BCD=2(∠1+∠2)=2×90°=180°;等量代换;同旁内角互补,两直线平行.
点评 本题考查的是平行线的判定,关键是利用同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:解答题
 推理填空
推理填空查看答案和解析>>
科目:初中数学 来源: 题型:解答题
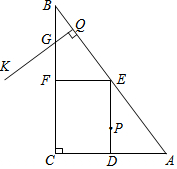 如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
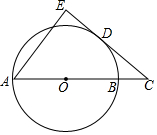 如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA
如图,AB是⊙O的直径,点C在AB的延长线上,D为圆上一点,连CD,且DC2=CB•CA查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com