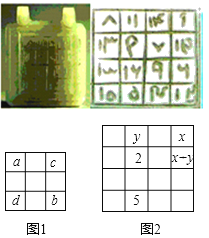
【题目】如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉﹣﹣明白玉幻方．其背面有方框四行十六格，为四阶幻方（从1到16，一共十六个数目，它们的纵列、横行与两条对角线上4个数相加之和均为34）．小明探究后发现，这个四阶幻方中的数满足下面规律：在四阶幻方中，当数a，b，c，d有如图1的位置关系时，均有a+b＝c+d＝17．如图2，已知此幻方中的一些数，则x的值为__．
黎明文化寒假作业系列答案科目：初中数学 来源： 题型：
【题目】如图，以正方形
的顶点
为坐标原点，直线
为
轴建立直角坐标系，对角线
与
相交于点
，
为
上一点，点坐标为
，则点绕点顺时针旋转90°得到的对应点的坐标是( )
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（7分）某市“艺术节”期间，小明、小亮都想去观看茶艺表演，但是只有一张茶艺表演门票，他们决定采用抽卡片的办法确定谁去．规则如下：
将正面分别标有数字1、2、3、4的四张卡片（除数字外其余都相同）洗匀后，背面朝上放置在桌面上，随机抽出一张记下数字后放回；重新洗匀后背面朝上放置在桌面上，再随机抽出一张记下数字．如果两个数字之和为奇数，则小明去；如果两个数字之和为偶数，则小亮去．
（1）请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果；
（2）你认为这个规则公平吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次，掷第一次，将朝上一面的点数记为
，掷第二次，将朝上一面的点数记为
，则点（
）落在直线
上的概率为：
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，四边形
是平行四边形，
，若
，
的长是关于
的一元二次方程
的两个根，且
.
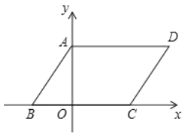
（1）直接写出：
______，
______；
（2）若点
为轴正半轴上的点，且
；
①求经过
，两点的直线解析式；
②求证：
.
（3）若点
在平面直角坐标系内，则在直线
上是否存在点
，使以
，
，，为顶点的四边形为菱形？若存在，直接写出点的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线y＝ax2﹣2ax+c（a≠0）与y轴交于点A，将点A向右平移1个单位长度，得到点B．直线y＝
x﹣3与x轴，y轴分别交于点C，D．
（1）求抛物线的对称轴；
（2）若点A与点D关于x轴对称，
①求点B的坐标；
②若抛物线与线段BC恰有一个公共点，结合函数图象，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．
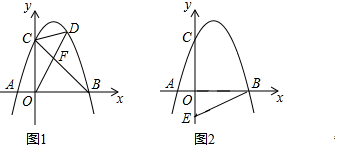
（1）求该抛物线的函数解析式；
（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD，OD交BC于点F，当S△COF：S△CDF＝3：2时，求点D的坐标．
（3）如图2，点E的坐标为（0，
），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
