
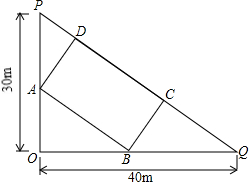
 如图所示,直角三角形内部有一矩形,求矩形的最大面积.
如图所示,直角三角形内部有一矩形,求矩形的最大面积.| 50OE |
| 2 |
| 30×40 |
| 2 |
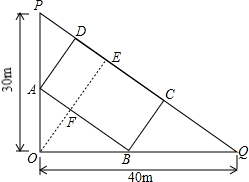
| OF |
| OE |
| AB |
| PQ |
| 24-x |
| 24 |
| AB |
| 50 |
| 25(24-x) |
| 12 |
| 25(24-x) |
| 12 |
| 25 |
| 12 |
| 25 |
| 12 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
| A、3cm,6cm,8cm |
| B、3cm,8cm,9cm |
| C、3cm,6cm,9cm |
| D、6cm,8cm,9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=18,CD=21,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=18,CD=21,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 7 |
| 25 |
| 25 |
| 7 |
| 25 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
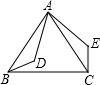 如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( )
如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( )| A、45° | B、60° |
| C、90° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
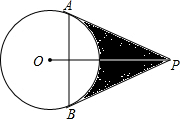 如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=| 3 |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
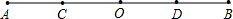 如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想:
如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想:查看答案和解析>>
科目:初中数学 来源: 题型:
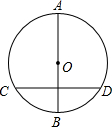 如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )
如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )| A、3 | B、2 | C、1 | D、0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com