
【题目】如图,BE是⊙O的直径,点A和点D是⊙O上的两点,连接AE,AD,DE,过点A作射线交BE的延长线于点C,使∠EAC=∠EDA.
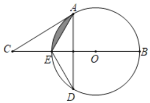
(1)求证:AC是⊙O的切线;
(2)若CE=AE=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)见解析;(2)2π-![]()
【解析】
(1)连接OA,过O作OF⊥AE于f,得到∠EAO+∠AOF=90°,根据等腰三角形的性质和圆周角定理得到∠EDA=∠AOF,推出OA⊥AC,得到AC是⊙O的切线;
(2)根据等腰三角形的性质得到∠C=∠EAC,得到∠AEO=2∠EAC,推出△OAE是等边三角形,根据扇形的面积公式得到S扇形AOE=![]() π,求得S△AOE=
π,求得S△AOE=![]() AEOF=
AEOF=![]() ×
×![]() ×3=
×3=![]() ,于是得到结论.
,于是得到结论.
解:(1)证明:连接OA,过O作OF⊥AE于F,
∴∠AFO=90°,
∴∠EAO+∠AOF=90°,
∵OA=OE,
∴∠EOF=∠AOF=![]() ∠AOE,
∠AOE,
∵∠EDA=![]() ∠AOE,
∠AOE,
∴∠EDA=∠AOF,
∵∠EAC=∠EDA,
∴∠EAC=∠AOF,
∴∠EAO+∠EAC=90°,
∵∠EAC+∠EAO=∠CAO,
∴∠CAO=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)解:∵CE=AE=![]() ,
,
∴∠C=∠EAC,
∵∠EAC+∠C=∠AEO,
∴∠AEO=2∠EAC,
∵OA=OE,
∴∠AEO=∠EAO,
∴∠EAO=2∠EAC,
∵∠EAO+∠EAC=90°,
∴∠EAC=30°,∠EAO=60°,
∴△OAE是等边三角形,
∴OA=AE,∠EOA=60°,
∴OA=![]() ,
,
∴S扇形AOE=![]() =2π,
=2π,
在Rt△OAF中,OF=OAsin∠EAO=![]() ×
×![]() =3,
=3,
∴S△AOE=![]() AEOF=
AEOF=![]() ×
×![]() ×3=
×3=![]() ,
,
∴阴影部分的面积=2π-![]() .
.


科目:初中数学 来源: 题型:
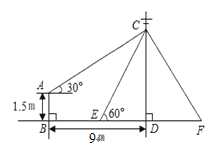
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点,则PA+PB的最小值为( )
的中点,P是直径MN上一动点,则PA+PB的最小值为( )

A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有五个小球,每个小球上面分别标着 1,2,3,4,5 这五个数字中的一个,这些小球除标的数字不同以外,其余的全部相同.把分别标有数字 4、5 的两个小球放入不透明的口袋 A 中,把分别标有数 字 1、2、3 的三个小球放入不透明的口袋 B 中.现随机从 A 和 B 两个口袋中各取出一个小球,把 从 A 口袋中取出的小球上标的数字记作 m,从B口袋中取出的小球上标的数字记作 n,且 m-n=k,则 y 关于 x 的二次函数 ![]() 与 x 轴有交点的概率是_________________.
与 x 轴有交点的概率是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东同学根据函数的学习经验,对函数y ![]()
![]() 进行了探究,下面是他的探究过程:
进行了探究,下面是他的探究过程:
(1)已知x=-3时![]() 0;x=1 时
0;x=1 时![]() 0,化简:
0,化简:
①当x<-3时,y=
②当-3≤x≤1时,y=
③当x>1时,y=
(2)在平面直角坐标系中画出y ![]()
![]() 的图像,根据图像,写出该函数的一条性质.
的图像,根据图像,写出该函数的一条性质.
(3)根据上面的探究解决,下面问题:
已知A(a,0)是x轴上一动点,B(1,0),C(-3,0),则AB+AC的最小值是

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com