
如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.
(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.

(1)见解析 (2)见解析
【解析】【解析】
(1)如图所示:

(2)四边形BFDE的形状是平行四边形,
理由如下:
∵在平行四边形ABCD中,∴∠DAC=∠ACB,AD=BC,
在△ADE和△CBF中,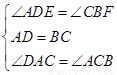
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°﹣∠AED,∠BFE=180°﹣∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形.
(1)作∠CBM=∠ADE,其中BM交CD于F即可;
(2)四边形BFDE的形状是平行四边形,连BE、DF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源:2014中考名师推荐数学转化思想(解析版) 题型:填空题
如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,则道路的宽为 .

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学概率(解析版) 题型:选择题
如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数的规律(解析版) 题型:填空题
一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,则63“分裂”出的奇数中,最大的奇数是 .
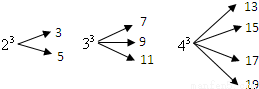
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=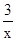 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
A.0<x0<1
B.1<x0<2
C.2<x0<3
D.﹣1<x0<0
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )

A.19°
B.38°
C.52°
D.76°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com