
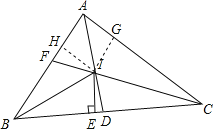
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I,IE⊥BC与E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】A
【解析】
①由I为△ABC三条角平分线的交点,IE⊥BC于E,得到∠ABI=∠IBD,由于∠CID+∠ABI=90°,即∠CIE+∠DIE+∠IBD=90°,于是得到∠BIE=∠CID;即①成立;②由I是△ABC三内角平分线的交点,得到点I到△ABC三边的距离相等,根据三角形的面积即可得到即②成立;③如图过I作IH⊥AB于H,IG⊥AC于G,有I是△ABC三内角平分线的交点,得到IE=IH=IG,通过Rt△AHT≌△RtAGI,得到AH=AG,同理BE=BF,CE=CG,于是得到即③成立;④由③证得IH=IE,∠FHI=∠IED=90°,于是得到△IHF与△DEI不一定全等,即④错误.
①∵I为△ABC角平分线的交点,IE⊥BC于E,
∴∠ABI=∠IBD,
∵∠DIC=∠DAC+∠ACI=![]() (∠BAC+∠ACB),∠ABI=
(∠BAC+∠ACB),∠ABI=![]() ∠ABC,
∠ABC,
∴∠CID+∠ABI=90°,
∵IE⊥BC于E,
∴∠BIE+∠IBE=90°,
∵∠ABI=∠IBE,
∴∠BIE=∠CID;
即①成立;
②∵I是△ABC三内角平分线的交点,
∴点I到△ABC三边的距离相等,
∴S△ABC=S△ABI+S△BCI+S△ACI=![]() ABIE+
ABIE+![]() BCIE+
BCIE+![]() ACIE=
ACIE=![]() IE(AB+BC+AC),即②成立;
IE(AB+BC+AC),即②成立;
③如图过I作IH⊥AB于H,IG⊥AC于G,
∵I是△ABC三内角平分线的交点,
∴IE=IH=IG,
在Rt△AHT与△RtAGI中,
![]() ,
,
∴Rt△AHT≌△RtAGI,
∴AH=AG,
同理BE=BH,CE=CG,
∴BE+BH=AB+BC-AH-CE=AB+BC-AC,
∴BE=![]() (AB+BC-AC);即③成立;
(AB+BC-AC);即③成立;
④由③证得IH=IE,
∵∠FHI=∠IED=90°,
∴△IHF与△DEI不一定全等,
∴HF不一定等于DE,
∴AC=AG+CG=AH+CE≠AF+CD,即④错误.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )

A. 2![]() B. 2
B. 2![]() C.
C. ![]() +1D.
+1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
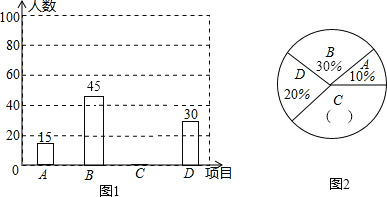
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是![]()
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得![]() 的图象
的图象
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC=4,将△ABC翻折,使得点A落在BC的中点A'处,折痕分别交边AB、AC于点D、点E,那么AD:AE的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
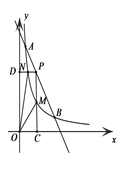
【题目】如图,一次函数与反比例函数的图像交于A(1,12)和B(6,2)两点。点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N,则四边形PMON面积的最大值是( )
A. ![]() B.
B. ![]() C. 6 D. 12
C. 6 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com