
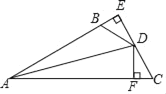
【题目】如图,AD平分∠EAC,DE⊥AB于E,DF⊥AC于F,BD=CD,
(1)求证:BE=FC;
(2)已知AC=20,BE=4,求AB的长.
【答案】(1)详见解析;(2)12
【解析】
(1)根据角平分线性质和全等三角形的性质即可解决问题;
(2)由△ADE≌△ADF(AAS),推出AF=AE,由BE=CF=4,AC=20,推出AF=AE=20﹣4=16即可解决问题;
(1)∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BED和Rt△CFD中
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)在△ADE和△ADF中,
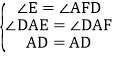 ,
,
∴△ADE≌△ADF(AAS),
∴AF=AE,
∵BE=CF=4,AC=20,
∴AF=AE=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I,IE⊥BC与E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3)
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)求出△A1B1C1的面积;
(3)将△ABC向左平移2个单位,再向上平移2个单位得△A2B2C2,请直接写出点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
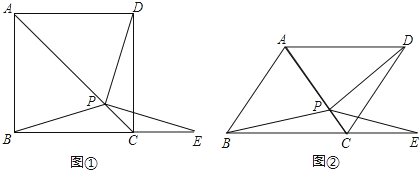
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
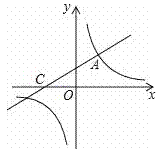
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
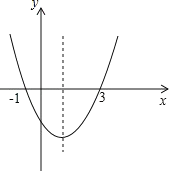
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某丝巾厂家70名工人义务承接了第十六届亚运会上中国志愿者手上、脖子上的丝巾的制作任务.已知每人每天平均生产手上的丝巾1800条或者脖子上的丝巾1200条,1条脖子上的丝巾要配2条手上的丝巾.
(1)为了使每天生产的丝巾刚好配套,应分配多少名工人生产手上的丝巾,多少名工人生产脖子上的丝巾?
(2)在(1)的方案中,能配成______套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先观察下列各式,再解答后面问题:
![]() =x2+11x+30;
=x2+11x+30;![]() =x2﹣11x+30;
=x2﹣11x+30;
![]() =x2+x﹣30;
=x2+x﹣30;![]() =x2﹣x﹣30;
=x2﹣x﹣30;
(1)根据以上各式呈现的规律,用公式表示出来,则![]() = ;
= ;
(2)试用你写的公式,直接写出下列两式的结果
①![]() = ;
= ;
②![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com