
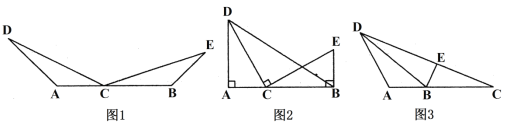
【题目】⑴如图1,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE,DC=CE.求证:AC=BE.
⑵如图2,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE=90°.
①求证:![]() ;②连接BD,若∠ADC=∠ABD,AC=3,BC=
;②连接BD,若∠ADC=∠ABD,AC=3,BC=![]() ,求tan∠CDB的值;
,求tan∠CDB的值;
⑶如图3,在△ABD中,点C在AB边上,且∠ADC=∠ABD,点E在BD边上,连接CE,∠BCE+∠BAD=180°,AC=3,BC=![]() ,CE=
,CE=![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用AAS证明![]() 可得AC=BE;
可得AC=BE;
(2)①先证明△DAC∽△CBE,再利用相似三角形的性质可得![]() ;
;
②根据∠A=∠DCE=∠CBE=90°,∠ADC=∠ABD,可推出△ADC∽△ADB,从而求出相应的线段长度,得到tan∠CDB的值.
(3)根据∠ADC=∠ABD,可推出△ADC∽△ADB,从而得到AD的长,根据∠BCE+∠BAD=180°,以E为圆心,EC长为半径画弧,交BC于点H,连接EH,可得EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,可得△BEH∽△ADC,则 .
.
(1)证明:如图1,
![]() ,
,![]()
又![]() ,
,![]()
![]()
又![]()
![]()
![]()
(2)①证明:∵∠DCA+∠DCE+∠ECB=180°,
∠DCA+∠A+∠CDA=180°,∠A=∠DCE,
∴∠ADC=∠ECB,
∵∠A=∠B,
∴△DAC∽△CBE,
![]()
②如图2,

∵∠ADC=∠DBA,∠A=∠A,
∴△ADC∽△ABD,
![]()
AB=AC+BC=![]()
∴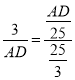
解得AD=5,
![]()
设∠DBA=∠CDA=α,
∴∠CDG=90-2α,
∴∠CGD=2α,
∴∠GCB=∠GBC=α,
∴CG=GB,
设CG=GB=x,
![]()

解得![]()
![]()
(3)如图3,

∵∠ADC=∠B,∠A=∠A,
∴△ADC∽△ADB,
![]()
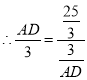
解得AD=5,
∵∠BCE+∠BAD=180°,∠ADC+∠DCA+∠BAD=180°,
∴∠ADC+∠DCA=∠BCE,
以E为圆心,EC长为半径画弧,交BC于点H,连接EH,
∴EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,
∵∠B=∠ADC,
∴∠BEH=∠ACD,
∴△BEH∽△ADC,
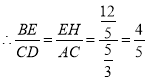
故答案为:![]()


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】十三五”以来,党中央,国务院不断加大脱贫攻坚的支持决策力度,并出台配套文件,国家机关各部门也出台多项政策文件或实施方案.某单位认真分析被帮扶人各种情况后,建议被帮扶人大力推进特色产业,大量栽种甜橙;同时搭建电商运营服务平台,开设网店销售农产品橙.丰收后,将一批甜橙采取现场销售和网络销售相结合进行试销,统计后发现:同样多的甜橙,现场销售可获利800元,网络销售则可获利1000元,网络销售比现场销售每件多获利5元
(1)现场销售和网络销售每件分别多少元?
(2)根据甜橙试销情况分析,现场销售量a(件)和网络销售量b(件)满足如下关系式:b=﹣![]() a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
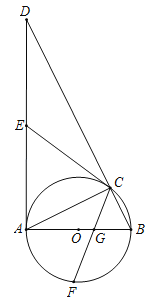
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 为直径
为直径![]() 下方半圆的中点,连接
下方半圆的中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中有1个白球和2个红球,这些球除颜色外都相同.
⑴如果从盒子中随机摸出1个球,摸出红色球的概率为_____________;
⑵若从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,请通过列表或画树状图的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
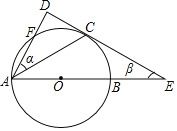
【题目】如图,已知⊙O的直径AB=10,AC是⊙O的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作AD⊥DE,垂足为D,与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β,且0°<α<45°.
(1)求β(用含α的代数式表示);
(2)连结OF交AC于点G,若AG=CG,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
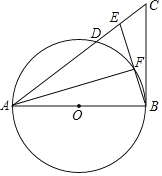
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:EF=BF;
(2)求证:BC是⊙O的切线.
(3)若AB=4,BC=3,求DE的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知将反比例函数![]() (x<0),沿y轴翻折得到反比例函数
(x<0),沿y轴翻折得到反比例函数![]() (x>0),一次函数y=ax+b与
(x>0),一次函数y=ax+b与![]() 交于A(1,m),B(4,n)两点;
交于A(1,m),B(4,n)两点;
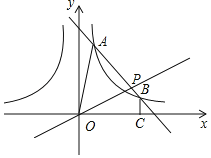
(1)求反比例函数y2和一次函数y=ax+b的解析式;
(2)连接OA,过B作BC⊥x轴,垂足为C,点P是线段AB上一点,若直线OP将四边形OABC的面积分成1:2两部分,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com